【深度学习】Attention is All You Need : Transformer模型

在transformer提出前，比如做机器翻译，常用的是seq2seq的模型。这类模型以RNN作为基本的结构，每一个时刻的输入依赖于上一个时刻的输出，难以并行化计算（当然也可以用CNN来做，如textCNN，CNN可以比较好的做到并行）；此外，RNN容易忘记较早看到的信息，尽管有LSTM、GRU使用门的机制来缓解这个问题，但对于特别长的句子，仍旧是有问题的。Transformer的提出正是解决了上述两个问题。

首先来看看Transformer的结构：

transformer

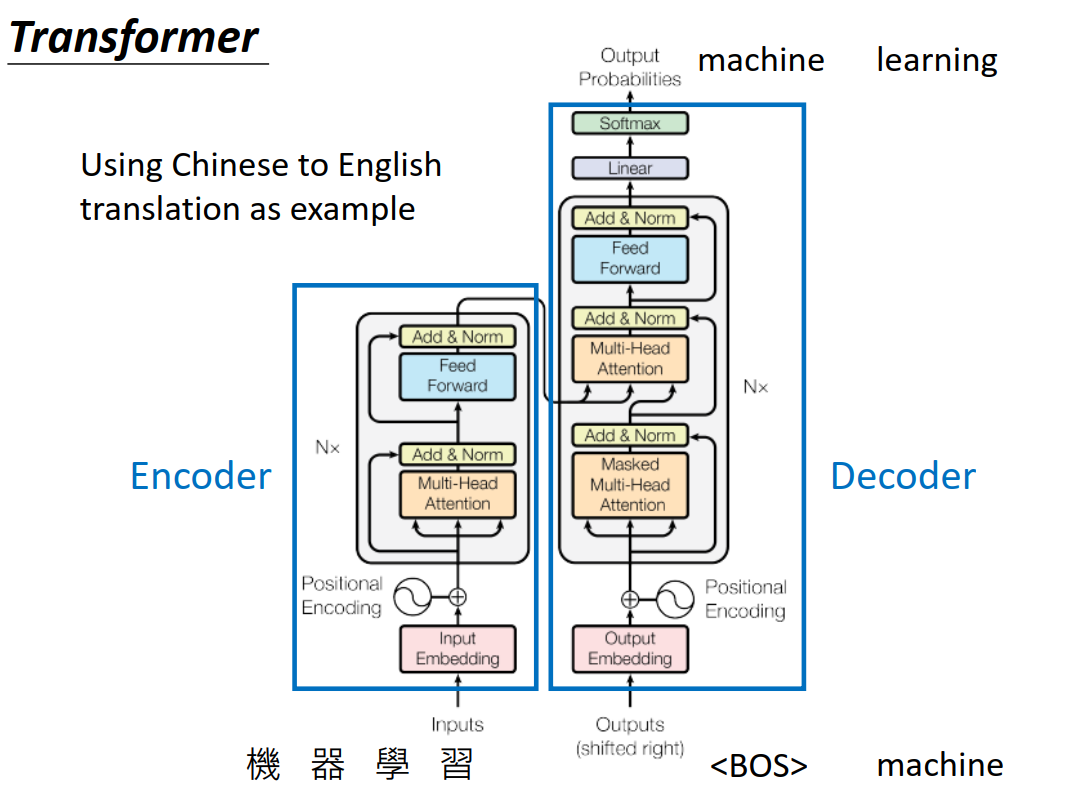
看上去很复杂，但大体上，也是分为Encoder和Decoder，以机器翻译为例，Encoder输入“机器学习",Decoder输出”Machine learning“。

下面对Encoder和Decoder分别进行讲解。不过在此之前，会先介绍Self-Attention机制，因为transformer中大量的采用了这个机制。

Self-Attention

想必在此之前，你已经听过了Seq2Seq模型中的Attention机制，那么它和Self Attetion有什么区别呢？我们先对了Seq2Seq模型中的Attention机制做一个简短的回顾，然后在切入主题。

Attetion in Seq2Seq model

前面提到过，seq2seq model在面对长句子的时候表现不佳，那么怎么办呢？2015年救星Attention诞生了。这个过程下面的图很生动的说明了这个情况：

seq2seq-model-to-attention

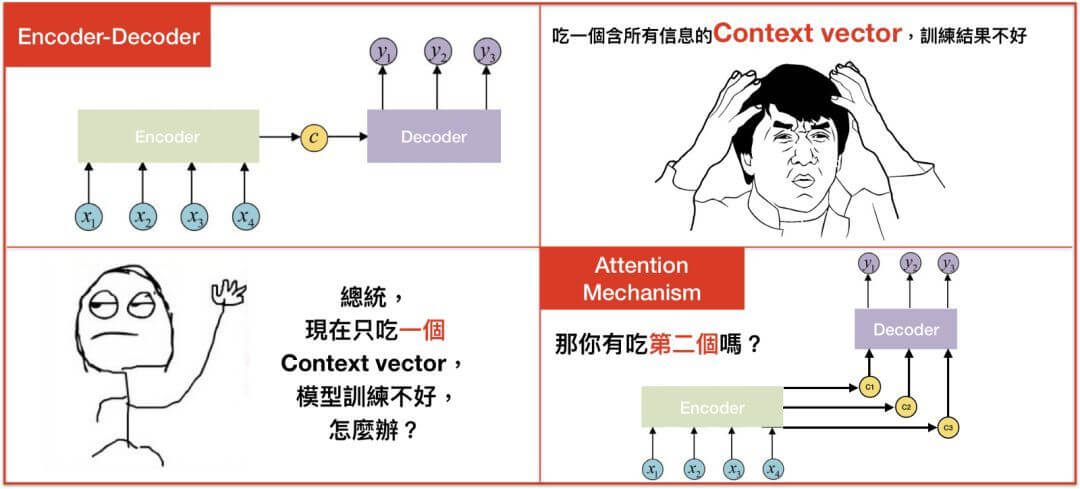
注意到，一开始的Encoder-Decoder将input的sequence都encode为一个向量，而有了attention之后，多了好几个向量。这几个向量是怎么来的呢？

这里借用李宏毅老师的PPT来向大家说明。Attention相当于权重，比如你要翻译某个词的时候，可能会更加的注意输入句子某几个词。

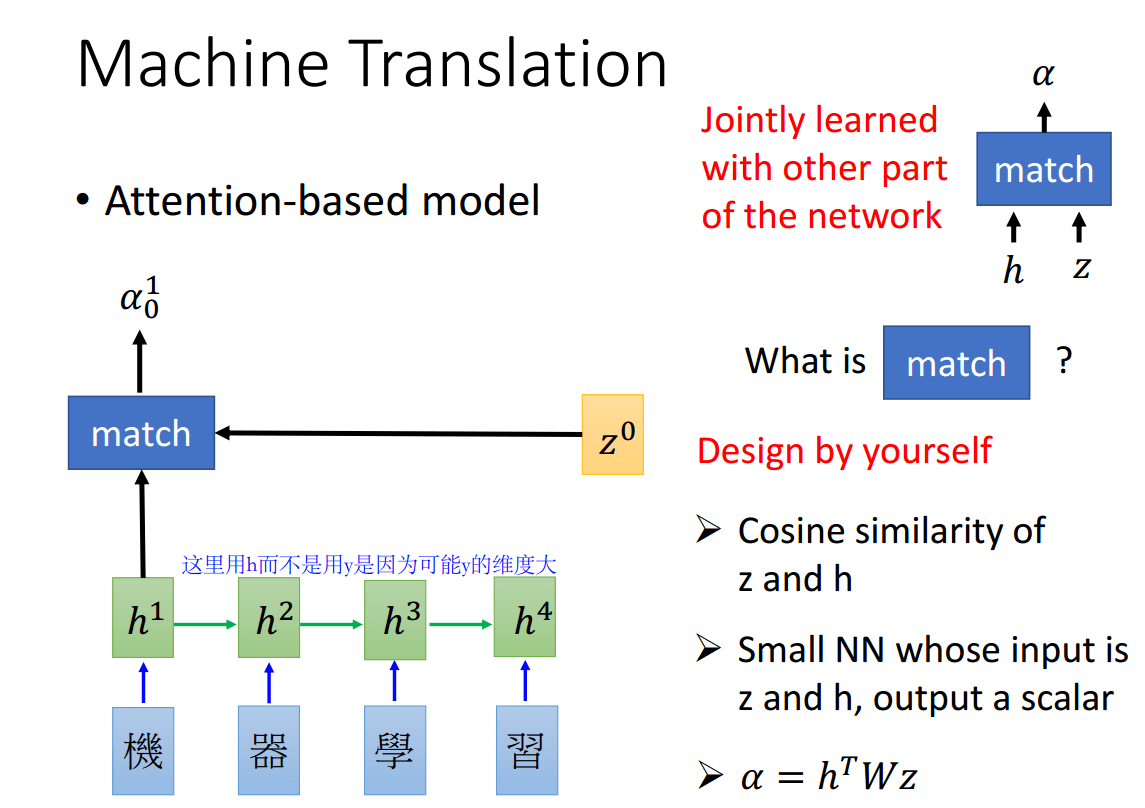
下面的\(h^1,h^2,h^3,h^4\)是对应的输出句子4个时刻的隐向量（而不是最后LSTM输出的y，因为y可能维度比较大），而\(\alpha_0^1\)则代表\(z^0\)和\(h^1\)的权重，即需要关注第一个词的程度有多少。

\(\alpha_0^1\)是怎么得到的呢？可以想象为一个黑盒，输入是\(h^1\)和\(z^0\)。中间的部分可以是简单的\(z\)和\(h\)的余弦距离，而可以是一个简单的网络。

seq2seq-attention1

对每个词都用\(z^0\)和\(h^i\)跑一遍，就得到了\(\alpha_0^1,\alpha_0^2,\alpha_0^3,\alpha_0^4\)，然后进行softmax概率归一化，得到\(\hat{a}_0^1，\hat{a}_0^2，\hat{a}_0^3，\hat{a}_0^4\)，接着和\(h^i\)相乘，就得到了\(c^0=\sum{\hat{a}_0^ih^i}\)，这个\(c^0\)就是Decoder的输入

seq2seq-attention2

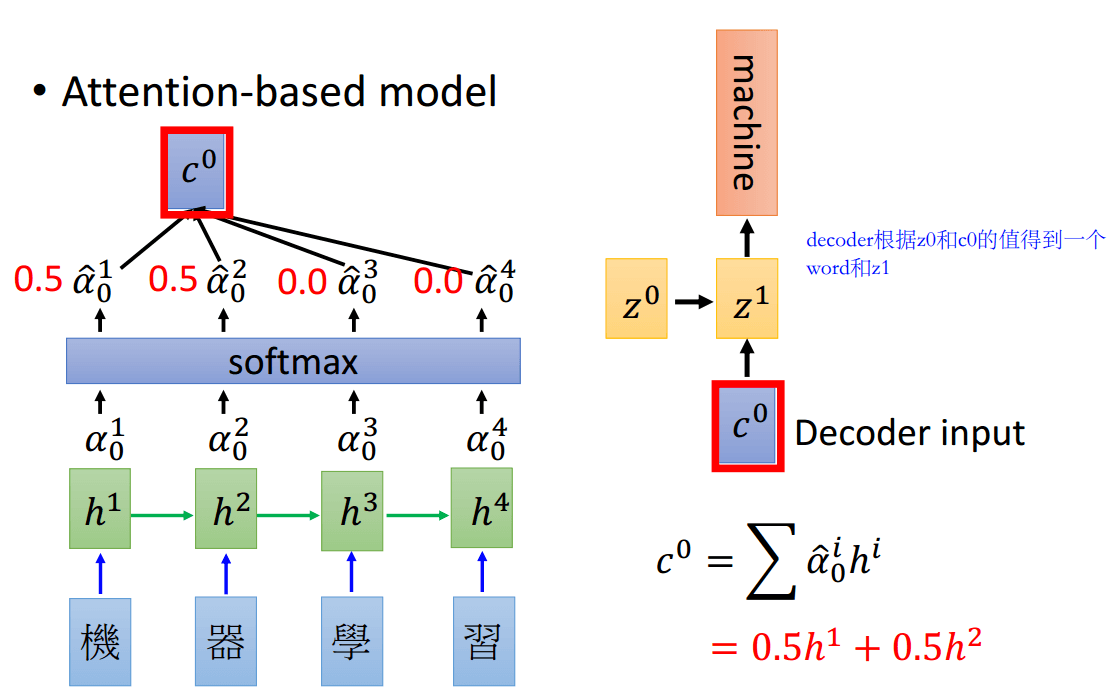
对输出的每个时刻都重复上述的过程，相当于每个时刻对每个输入的x的权重是不一样的，得到的c也是不一样的。

seq2seq-attention3

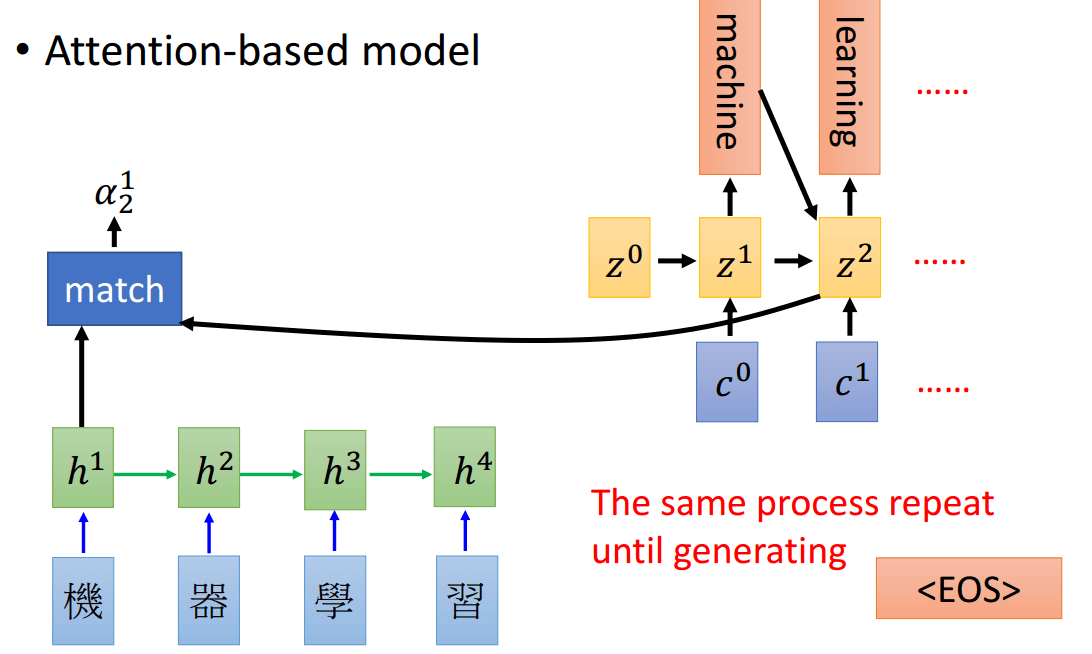
这就是Seq2seq中的attention，简单的说就是细化Decoder每个时刻需要注意的x，从而得到不同的Decoder输入\(c^i\)

self-attention

那么self attention是怎么样做的呢？

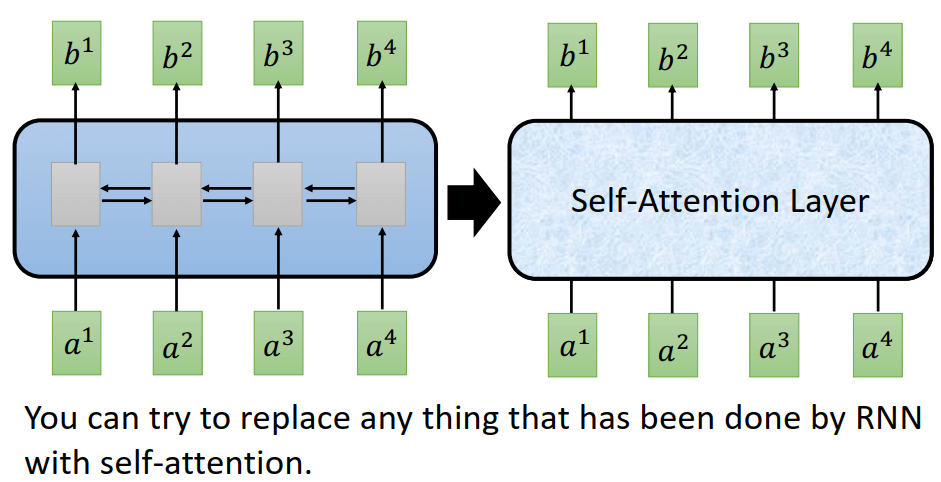
来个直观的印象：左边的是RNN，有4个时刻，每个时刻输出一个b。而右边是Self-attention，它的输出也是4个b，但是这个是并行的计算的！

replace-rnn-by-self-attention

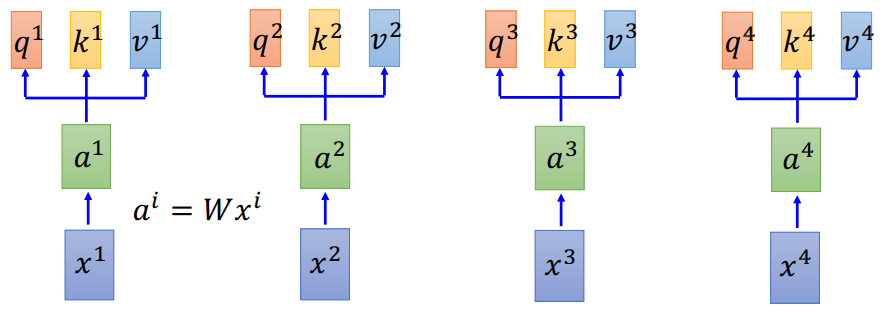
这是怎么做的呢？回想之前Encoder和Decoder的权重是由Decoder的状态\(z\)乘以encoder的输出\(h\)得到的，而self-attention比较巧妙的地方就在于将每个输入x都先做一个线性变化\(a^i = Wx^i\)，然后每个\(a^i\)都分成了3个子向量\(q^i, k^i, v^i\)，分别代表query，key，和value。（在实际的实现中，可以认为q，k, v分别是由3个不同的W乘上x得来）

self-attention-q-k-v

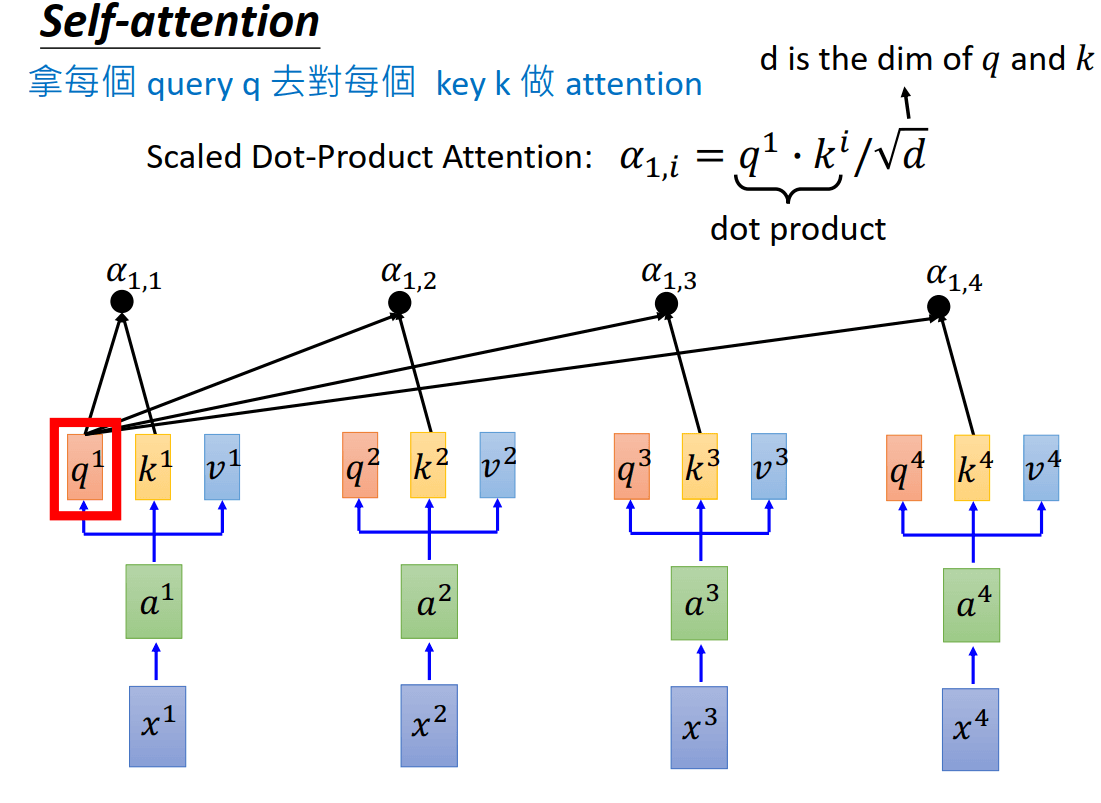
然后拿每个query去对每个key做attention，得到\(a_{1,i} = q^1\cdot k^i/\sqrt{d}\)。其中d是q和k的维度，这里除以\(\sqrt{d}\)是因为为了防止后过q和k随着维度的增长点积结果过大。

self-attention-q-k-v2

接下来也对各个\(\alpha_{1,i}\)做softmax，得到\(\hat{a}_{1,i}\)，然后每个\(\hat{a}_{1,i}\)和对应的\(v^i\)相乘并加起来，得到输出\(b^1 = \sum_{i}\hat{a}_{1,i}v^i\)。用RNN的话说，这就是在时刻1得到的输出，并且这个输出考虑了整个句子。

self-attention-q-k-v3

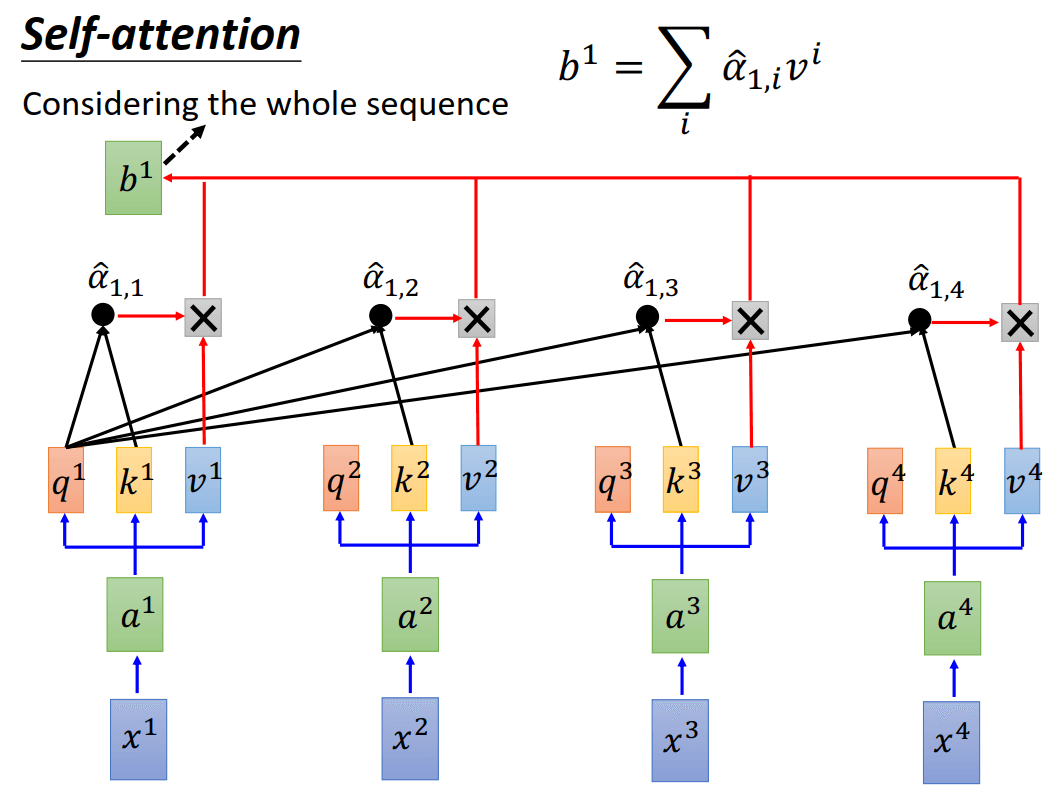
用\(q^2\)和其他的\(k^i\)相乘，也就得到了\(a_{2,i}\)。

这里简单的做一个和Encoder-Decoder中attention的对比：

• Encoder-Decoder将Decoder中的隐向量\(z^i\)和Encoder的隐向量\(h^i\)做相似度计算，得到\(a^{j}_i\)，表示\(i\)时刻对第\(j\)个词的关注程度。然后将同一时刻的\(a_i^j\)归一化得到\(\hat{a}^j_i\)，并和各个对应的隐向量做加权和，得到Decoder的输入\(c^i=\sum{\hat{a}_0^1h^i}\)。
• 而Self-attention则是首先做一个简单的线性变换，得到\(a^i = Wx^i\)，并将\(a^i\)分为三个分量\(q^i,k^i,v^i\)，分别代表query，key，和value。拿每个query去对每个key做attention，得到\(a_{1,i} = q^1\cdot k^i/\sqrt{d}\)， 然后softmax归一化，并和对应的value做加权和，得到输出\(b^1 = \sum_{i}\hat{a}_{1,i}v^i\)

可以看出，两个比较类似，Self-attention将Query和Key进行match，得到相应的权重，这大概是叫做”self"的原因。

self-attention 并行化

前面提到过，self-attention能够并行化的计算，这是怎么做到的呢？其实就是用到了矩阵的乘法而已。

前面得到的query、key、value，很容易就能并行，那么计算attention的时候呢？对于同一时刻\(a_{i,j}\)来说容易用矩阵一下子得出： \[ \begin{bmatrix} \alpha_{1,1}\\ \alpha_{1,2}\\ \alpha_{1,3}\\ \alpha_{1,4} \end{bmatrix} = \begin{bmatrix} k^1 \\k^2\\k^3\\k^4\end{bmatrix} q^1 \] 而不同时刻的权重类似的能这样得到（这里为了简单，省去了除以\(\sqrt{d}\)）： \[ \begin{bmatrix} \alpha_{1,1} & \alpha_{2,1} & \alpha_{3,1}& \alpha_{4,1}\\ \alpha_{1,2}& \alpha_{2,2} & \alpha_{3,2}& \alpha_{4,2}\\ \alpha_{1,3}& \alpha_{2,3} & \alpha_{3,3}& \alpha_{4,3}\\ \alpha_{1,4} & \alpha_{2,4} & \alpha_{3,4}& \alpha_{4,4}\\ \end{bmatrix} = \begin{bmatrix} k^1 \\k^2\\k^3\\k^4\end{bmatrix} \begin{bmatrix} q^1 & q^2 &q^3 &q^4\end{bmatrix} \] 即\(A = K^TQ\)，然后\(A\)也容易进行softmax得到\(\hat{A}\)，然后要得到输出，只需要： \[ \begin{bmatrix} b^1 & b^2 & b^3 & b^4\end{bmatrix} = \begin{bmatrix} v^1 & v^2 &v^3 &v^4\end{bmatrix} \begin{bmatrix} \hat{\alpha}_{1,1} & \hat{\alpha}_{2,1} & \hat{\alpha}_{3,1}& \hat{\alpha}_{4,1}\\ \hat{\alpha}_{1,2}& \hat{\alpha}_{2,2} & \hat{\alpha}_{3,2}& \hat{\alpha}_{4,2}\\ \hat{\alpha}_{1,3}& \hat{\alpha}_{2,3} & \hat{\alpha}_{3,3}& \hat{\alpha}_{4,3}\\ \hat{\alpha}_{1,4} & \hat{\alpha}_{2,4} & \hat{\alpha}_{3,4}& \hat{\alpha}_{4,4}\\ \end{bmatrix} \] 即\(B = V \hat{A}\)

这就得到了所有的输出。

Multi-head self-attention

Multi-head这个又是什么呢？

其实就是将原来的\(q^i, k^i, v^i\)分为多个，比如两个head的话，则query分为\(q^{1,i}, q^{i,2}\)，则key分为\(k^{i,1}, k^{i,2}\)，则value分为\(v^{i,1}, v^{i,2}\)

第一个头的q和第一个头的k做self-attention，如下图所示。

multi-head-attention

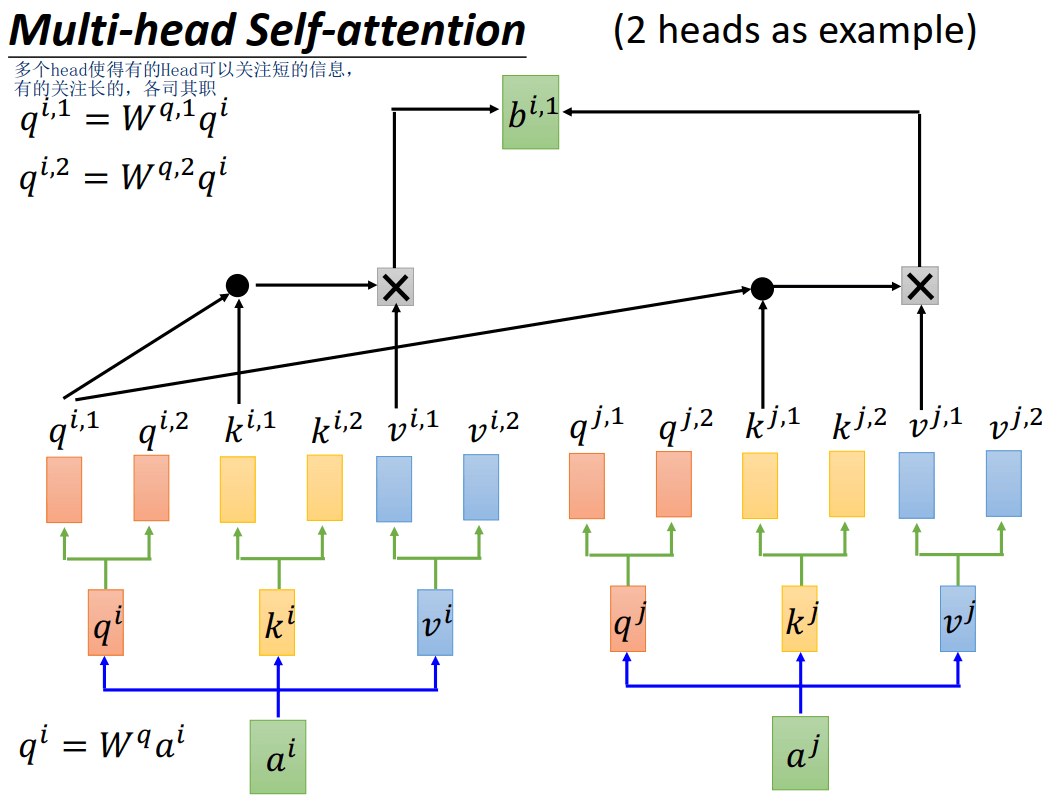
用多个head使得有的head可以关注短的信息，而有的关注长的，各司其职。

Multi-head self-attention 代码实现

这里介绍pytorch的实现，首先是计算attention的过程即上面的query、key、和value之间的计算，它们的维度都是[n_batch, head_num, seq_len, d_each_head]，分别代表batch_size的大小，multi-head中head的个书，句子的长度，每个head的向量维度（如\(q^{i,1}\)的长度），mask的作用下面在讲，可以先当作None处理。返回的向量也是[n_batch, head_num, seq_len, d_each_head]的维度

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

而pytorch类前向传播可以写为：

def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)

h, d_model代表head的个数，模型隐向量，如512。在forward中query, key, value的维度为：[n_batch, seq_len, d_model。在forward中：

1. 首先对query, key, value分别做线性变换, 即l(x)，然后将维度转为[n_batch, seq_len, head_num, d_each_head]，即l(x).view(nbatches, -1, self.h, self.d_k). 将第1维度和第2维度交换得到维度[n_batch, head_num, seq_len, d_each_head]
2. 然后调用attention函数，就得到了attention的输出，就是上面讲解的B，维度为[n_batch, head_num, seq_len, d_each_head]
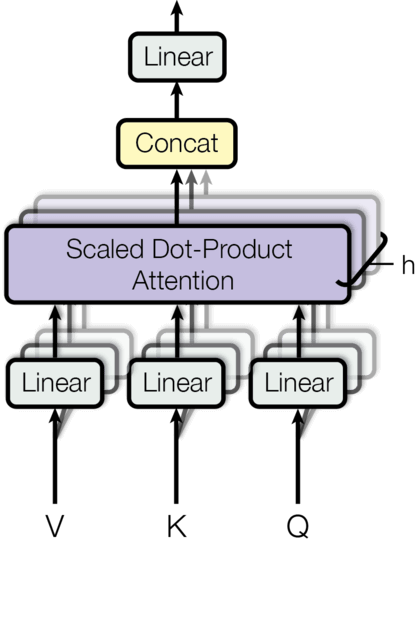
3. 最后将他们concat起来，得到维度[n_batch, seq_len, d_model]，然后在做线性的变换

整个过程如下面的图所示

multi-head-attention-pytorch

Transformer Encoder

讲完了self attention，就可以来讲Encoder的部分了：

transformer-encoder

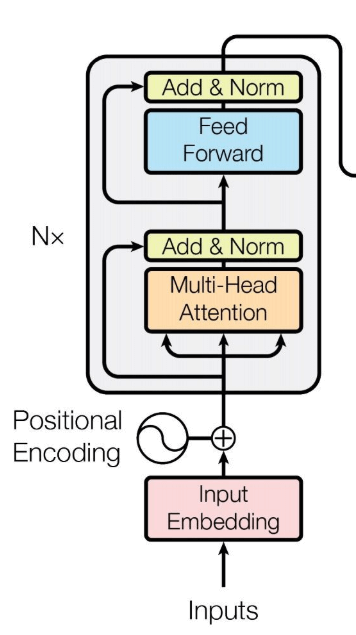
输入

首先输入经过embedding

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

然后会有一个Positional Encoding，这个是因为self-attention完全是并行计算的，并没有考虑句子中word的排序和位置信息，就是说a b c和c b a是完全一样的。（而RNN是按照顺序对句子处理的，当前时刻有上一个时刻的hidden state）。

因此在transform中作者提出加入位置信息的编码。将位置信息的编码加上embedding后的结果就得到了最终的模型输入。那么具体是怎么做的呢？作者探索了下面两种方式：

1. 通过训练学习 positional encoding 向量
2. 使用公式来计算 positional encoding向量

最终效果差不多，因此采用了第二种，因为不用通过训练，且即使在训练集中没有出现过的句子长度上也能用。

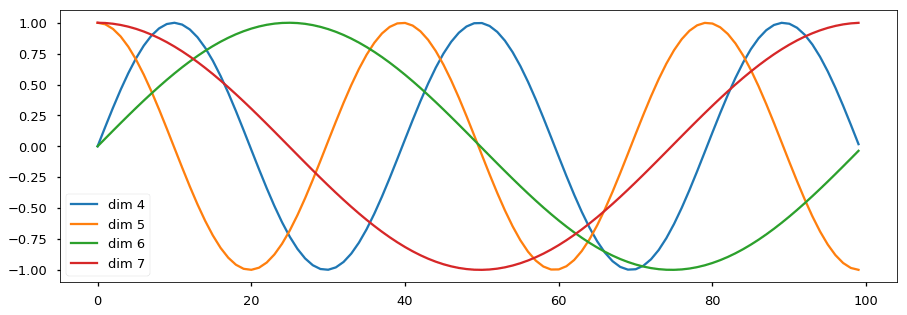
具体的公示为： \[ PE_{pos, 2i} = \sin(pos / 10000^{2i/d_{model}})\\ PE_{pos, 2i + 1} = \cos(pos / 10000^{2i/d_{model}}) \] pos代表word在这个句子中的位置，i代表模型的维度，从\([0...d_{model} - 1]\)

为什么选择 sin 和 cos ？positional encoding 的每一个维度都对应着一个正弦曲线，作者假设这样可以让模型相对轻松地通过对应位置来学习。

class PositionalEncoding(nn.Module):
    "Implement the PE function."
    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)
        
        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2) *
                             -(math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)
        
    def forward(self, x):
        x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
        return self.dropout(x)

波的频率和偏移对每个维度是不同的

positional-encoding

Encoder Layer细节

上面的encoder的图中，注意到旁边有个N x, 这表明这部分其实是可以重复多次的，在论文中是重复了6次：第1个encoder的输出作为第2个encoder的输入，如此循环。而每个Encoder中包含两个sub-layer，一个是multi-head-attention，一个是简单的全连接网络(feed forward)

下面的代码定义了Eecoder，将sub-layer重复了N次，forward的过程也很简单，每一次的输出作为下一次的输入，最后用LayerNorm得到输出。

class Encoder(nn.Module):
    "Core encoder is a stack of N layers"
    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

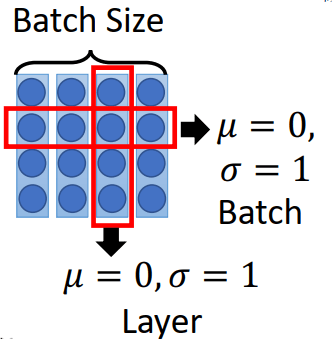
LayerNorm是Hinton发表的，有些类似Batch Normalization，Batch Normalization是对同一个batch下不同数据的同一纬度进行norm的，而layer则是对同一条data做的，区别见下面的图：

batch-normalization-vs-layer-normalization

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

此外，还引入了SublayerConnection（上面图中的Add & Norm），即类似ResNet的残差连接。因此每一个sub layer的输出为：\(\mathrm{LayerNorm}(x + \mathrm{Sublayer}(x))\)

class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """
    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

最后是sublayer的具体定义：先进行self-attention 子层，然后用feed_forward子层，每个子层都会用SublayerConnection连接一下。

class EncoderLayer(nn.Module):
    "Encoder is made up of self-attn and feed forward (defined below)"
    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
        "Follow Figure 1 (left) for connections."
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

其中，self_atten之前已经讲过，是之前定义的MultiHeadedAttention类，feed_forward定义如下: \[ FFN(x) = max(0, xW_1 + b_1) W_2 + b_2 \] 其实就是两个全连接层。

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x))))

Encoder 小结

Encoder 包含6个 EncoderLayer。每一个 EncoderLayer包含Multi-Headed Attention和Feed Forward两个sub-layer，subLayer还用SublayerConnection进行类似残差网络的连接。

Transformer Decoder

接下来是Decoder的部分：

transformer-decoder

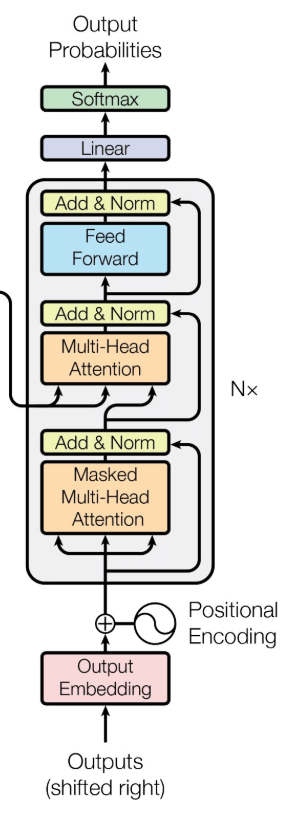
如果你弄懂了Encoder部分，Decoder部分也就没有那么可怕了：

1. 输入也是 embedding + positional Encoding，
2. 多层堆叠起来的(论文中为6)，每一层包含三个子层
   1. masked multi-head attention：由于在机器翻译中，Decode的过程是一个顺序的过程，也就是当解码第k个位置时，我们只能看到第k - 1 及其之前的解码结果，因此加了mask，这是防止模型看到要预测的数据。
   2. Multi-Head Attention：和Encoder的类似，6层中都接受Encoder的最后输出，作为key和value？
   3. FeedForward：和Encoder一样
3. 最后连接了LinearLayer和SoftmaxLayer

因此，这里先给出Decoder的定义：

class Decoder(nn.Module):
    "Generic N layer decoder with masking."
    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)
        
    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

可以看到，相比Encoder到多了mask的标识，

而DecoderLayer的定义为三个子层，中间也用SublayerConnection连接起来

class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"
    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)
 
    def forward(self, x, memory, src_mask, tgt_mask):
        "Follow Figure 1 (right) for connections."
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

Masked Multi-Headed Attention

这里对mask的过程做一个介绍，首先定义函数subsequent_mask

def subsequent_mask(size):
    "Mask out subsequent positions."
    attn_shape = (1, size, size)
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
    return torch.from_numpy(subsequent_mask) == 0

这个函数会形成一个下三角矩阵，用来说明每个target word（行）允许看的列，未来的word不被允许看到。

subsequent_mask(5)[0].int()
output:
tensor([[1, 0, 0, 0, 0],
        [1, 1, 0, 0, 0],
        [1, 1, 1, 0, 0],
        [1, 1, 1, 1, 0],
        [1, 1, 1, 1, 1]], dtype=torch.int32)

那么怎么用呢？

其实细心的读者会发现DecoderLayer的forward函数中，有src_mask, tgt_mask，他们是什么区别呢？前者是原文是否为pad（NLP经常会打pad使得句子长度一样），而后者就是之前说的不能看到未来的词，可以看Batch生成的代码：

class Batch:
    "Object for holding a batch of data with mask during training."
    def __init__(self, src, trg=None, pad=0):
        self.src = src
        self.src_mask = (src != pad).unsqueeze(-2)
        if trg is not None:
            self.trg = trg[:, :-1]
            self.trg_y = trg[:, 1:]
            self.trg_mask = \
                self.make_std_mask(self.trg, pad)
            self.ntokens = (self.trg_y != pad).data.sum()
    
    @staticmethod
    def make_std_mask(tgt, pad):
        "Create a mask to hide padding and future words."
        tgt_mask = (tgt != pad).unsqueeze(-2)
        tgt_mask = tgt_mask & Variable(
            subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
        return tgt_mask

完整的模型

到这里，就可以给出整个模型的代码了：

class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many 
    other models.
    """
    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator
        
    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        return self.decode(self.encode(src, src_mask), src_mask,
                            tgt, tgt_mask)
    
    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)
    
    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

Generator就是之前说的LinearLayer + SoftMaxLayer

class Generator(nn.Module):
    "Define standard linear + softmax generation step."
    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        return F.log_softmax(self.proj(x), dim=-1)

创建模型的helper函数：

def make_model(src_vocab, tgt_vocab, N=6, 
               d_model=512, d_ff=2048, h=8, dropout=0.1):
    "Helper: Construct a model from hyperparameters."
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), 
                             c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab))
    
    # This was important from their code. 
    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform(p)
    return model

tmp_model = make_model(10, 10, 2)

小结

个人认为Transformer的设计非常的巧妙，尤其是Self-attention layer，这使得原来并排的一个RNN可以用一个self-attetion layer替代，并且效率非常的高。Transformer影响了后面的很多模型，包括刷新了11个NLP领域方向记录大名鼎鼎的BERT，但BERT本质上是基于Transformer的预训练，个人认为不如Transformer创新度高。

这里引用知乎刘岩的做一个小结：

优点：（1）虽然Transformer最终也没有逃脱传统学习的套路，Transformer也只是一个全连接（或者是一维卷积）加Attention的结合体。但是其设计已经足够有创新，因为其抛弃了在NLP中最根本的RNN或者CNN并且取得了非常不错的效果，算法的设计非常精彩，值得每个深度学习的相关人员仔细研究和品位。（2）Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是1，这对解决NLP中棘手的长期依赖问题是非常有效的。（3）Transformer不仅仅可以应用在NLP的机器翻译领域，甚至可以不局限于NLP领域，是非常有科研潜力的一个方向。（4）算法的并行性非常好，符合目前的硬件（主要指GPU）环境。

缺点：（1）粗暴的抛弃RNN和CNN虽然非常炫技，但是它也使模型丧失了捕捉局部特征的能力，RNN + CNN + Transformer的结合可能会带来更好的效果。（2）Transformer失去的位置信息其实在NLP中非常重要，而论文中在特征向量中加入Position Embedding也只是一个权宜之计，并没有改变Transformer结构上的固有缺陷。

参考资料

1. The Annotated Transformer (推荐，本文的代码来自该链接)
2. 10分钟带你深入理解Transformer原理及实现
3. 详解Transformer （Attention Is All You Need）
4. 从Seq2seq到Attention模型到Self Attention（一）