『我爱机器学习』EM算法

EM算法即期望最大化算法(Expectation-Maximum）算法，它用于含有因变量的概率模型参数的极大似然估计，或极大后验估计。很多机器学习算法采用它进行求解，如高斯混合模型、LDA主题模型的变分推断等。

EM算法的引入

下面的例子来自[1]。

极大似然估计

假设有两枚硬币A和B，每次选一个硬币来抛10次。现在已经进行了5轮（也就是选了5次硬币，并分别抛了10次）结果如下（H表示正面，T表示反面）：

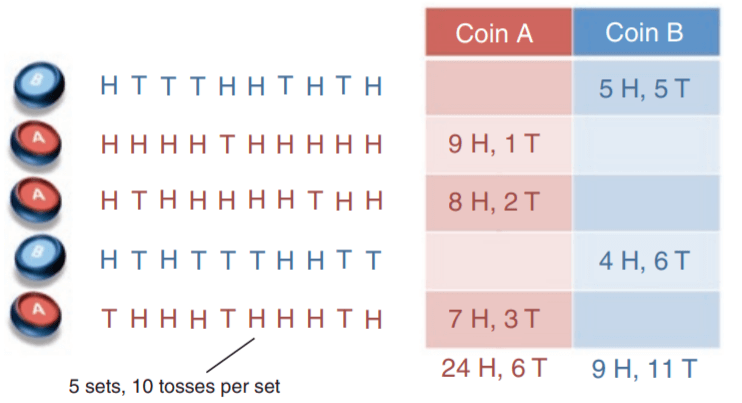
现在要求抛一次硬币A和硬币B正面朝上的概率（已知选的是A或者B硬币，求正面的概率），则我们可以简单的用极大似然估计来求解：

以硬币A的概率为例，抛硬币结果满足二项分布，可以写出似然函数： \[ \begin{align*} L &= \prod_{i=1}^{30}{\hat P_A}^{y_i}({1 -\hat P_A})^{(1- y_i)} \\ &= \hat{P_A}^{24}({1 -\hat{P_A} })^{6} \end{align*} \] 令其倒数为0，则有 \[ \frac{\partial L}{\partial \hat P_A} = 24{P_A}^{23}({1 -\hat{P_A} })^{6} - 6{P_A}^{24}({1 -\hat{P_A} })^{5}= 0\\ \] 可得\(\hat{P_A} = \frac{4}{5} = 0.80\)，这和我们直觉的计算是一样的，同理可以计算\(\hat{P_B}\)： \[ \hat P_A = \frac{24}{24 + 6} = 0.80\\ \hat P_B = \frac{9}{9 + 11} = 0.45 \]

EM 算法

现在让例子更复杂一点，假设我们每一轮不知道选的是硬币A还是硬币B，只知道每一轮10次的结果：

硬币	正面数	反面数
？	5	5
？	9	1
？	8	2
？	4	6
？	7	3

现在仍然要求抛一次硬币A和硬币B正面的概率，怎么做呢？

这个时候相当于有隐变量 \(\{\bf z_1, z_2, z_3, z_4, z_5\}\)，控制着我们每一轮抛硬币的时候是选择硬币A还是硬币B，比如\(\bf z_1\)代表第一轮投掷的时候使用硬币是A还是B。但是这个隐变量\({\bf z}\)我们是不知道的，也就无法用极大似然估计法来估计\(\hat P_A\)和\(\hat P_B\)。然而如果我们要估计隐变量\({\bf z}\)，那么我们又需要知道\(\hat P_A\)和\(\hat P_B\)。这使得这个问题进入了死循环，因为我们既不知道隐变量\(\bf z\), 也不知道\(\hat P_A\)和\(\hat P_B\)。

这时候EM算法就出来救场啦。EM算法的步骤如下：

随机初始化\(\hat P_A^{(0)}\)和\(\hat P_B^{(0)}\)
用\(\hat P_A^{(0)}\)和\(\hat P_B^{(0)}\)估计隐变量\(\bf z\)
根据估计出的隐变量\(\bf z\)来估计\(\hat P_A^{(1)}\)和\(\hat P_B^{(1)}\)
重复2-3步直到P不再变化或变化较小

现在我们来尝试手工计算一下，假设我们初始化\(\hat P_A^{(0)} = 0.60\)和\(\hat P_B^{(0)}= 0.50\)，现在来用极大似然法估计隐变量\(\bf z\)。

对于第一轮，如果是硬币A，可以计算出生成的概率为\(a = 0.6^5(1-0.6)^5=0.0007962624\), ，同理得如果是硬币B\(b = 0.5^5(1-0.5)^5=0.0009765625\)，这个值越大，说明越有可能使用该硬币。

则使用硬币A的概率为\(a / (a + b) = 0.45\), 使用硬币B的概率为\(b / (a + b) = 0.55\)。

接着根据估计出的隐变量\(\bf z\)来估计\(\hat P_A^{(1)}\)和\(\hat P_B^{(1)}\)：我们来计算一下以0.45的概率选择硬币A，0.55的概率选择硬币B时，5个为正的结果中有\(0.45 * 5 = 2.25\)是A“产生"的，有\(0.55 * 5 = 2.75\)个是B”产生"的。以此类推，可以得到下面的表格：

选择A的概率	A的正面贡献	A的反面贡献	选择B的概率	B的正面贡献	B的反面贡献
0.45	2.25	2.25	0.55	2.75	2.75
0.80	7.24	0.8	0.20	1.76	0.20
0.73	5.87	1.47	0.27	2.13	0.53
0.35	1.41	2.11	0.65	2.59	3.89
0.65	4.53	1.94	0.35	2.47	1.06

统计得到：A总共有21.3次正面，8.6次反面，B有11.7次正面，8.4次反面，因此更新新的概率 \[ \hat P_A^{(1)} = \frac{21.3}{21.3+8.6} \approx 0.71\\ \hat P_B^{(1)} = \frac{11.7}{11.7+8.4} \approx 0.58 \] 重复上面的过程，到第10次的时候收敛有: \[ \hat P_A^{(10)} \approx 0.80\\ \hat P_B^{(10)} \approx 0.52 \] 用下面的代码来计算表示:

class EMSolve(object):
    def __init__(self, pa, pb, max_round=100):
        self.heads_cnt = [5, 9, 8, 4, 7]  # 正面次数
        self.round_num = 10
        self.pa = pa
        self.pb = pb
        self.max_round = max_round

    def e_step(self):
        a_cnt = []
        b_cnt = []
        for pos_cnt in self.heads_cnt:
            likelihood_a = (self.pa ** pos_cnt) * ((1 - self.pa) ** (self.round_num - pos_cnt))
            likelihood_b = (self.pb ** pos_cnt) * ((1 - self.pb) ** (self.round_num - pos_cnt))
            choose_a = likelihood_a / (likelihood_a + likelihood_b)
            choose_b = likelihood_b / (likelihood_a + likelihood_b)
            a_cnt.append([choose_a * pos_cnt, choose_a * (self.round_num - pos_cnt)])
            b_cnt.append([choose_b * pos_cnt, choose_b * (self.round_num - pos_cnt)])
            # print('a: ', round(choose_a, 2), round(a_cnt[-1][0], 2), round(a_cnt[-1][1], 2), '\tb:', round(choose_b, 2), round(b_cnt[-1][0], 2), round(b_cnt[-1][1], 2))
        return a_cnt, b_cnt

    def m_step(self, a_cnt, b_cnt):
        total_a = sum(sum(x) for x in a_cnt)
        new_a = sum(x[0] for x in a_cnt) / total_a

        total_b = sum(sum(x) for x in b_cnt)
        new_b = sum(x[0] for x in b_cnt) / total_b

        return new_a, new_b

    def start(self):
        for epoch in range(self.max_round):
            a_cnt, b_cnt = self.e_step()
            new_pa, new_pb = self.m_step(a_cnt, b_cnt)
            print(epoch, new_pa, new_pb)
            if abs(new_pa - self.pa) < 1e-4 and abs(new_pb - self.pb) < 1e-4:
                break
            self.pa, self.pb = new_pa, new_pb

if __name__ == '__main__':
    EMSolve(pa=0.6, pb=0.5).start()

那么，上面的做法的理论依据是什么呢？是不是一定能收敛到最优解呢？请继续往下阅读。

数学基础

首先来介绍一点之后要用到的数学基础。

凸函数 Convex functions

凸函数的数学定义为：在某个向量空间的凸子集C上的实值函数\(f\)，如果在其定义域\(C\)上的任意两点\(x_1,x_2\)以及\(\lambda \in [0,1]\)，有

\[ f(\lambda x_1+(1-\lambda )x_2) \le \lambda f(x_1) + (1-\lambda )f(x_2)\tag{2-1} \] 如果对于任意的\(\lambda \in (0,1)\)，有\(f(\lambda x_1+(1-\lambda )x_2) \lt \lambda f(x_1) + (1-\lambda )f(x_2)\),则称\(f\)是严格凸的。

上面的定义说明凸函数任意两点的连线位于图形的上方。

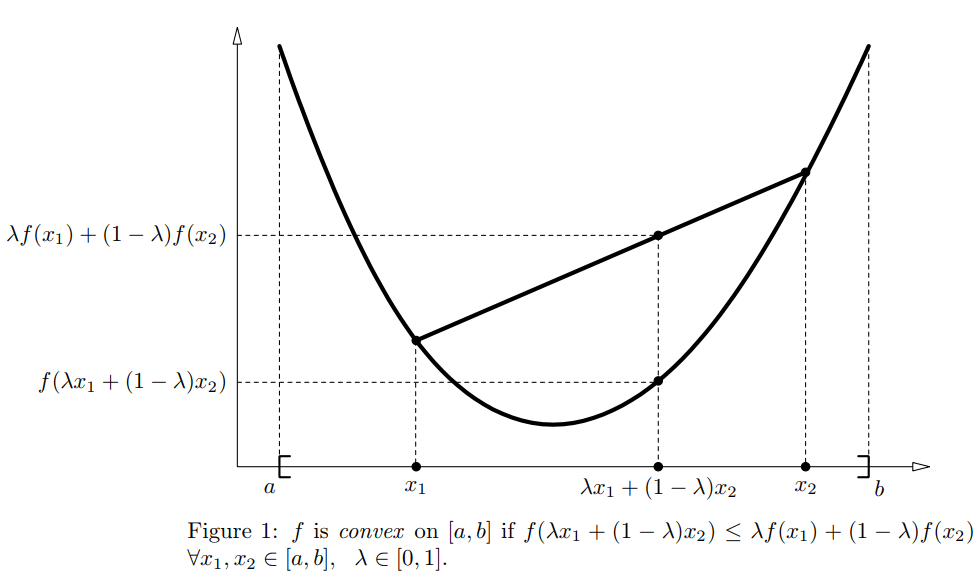
此外，假设\(f\)是二阶可微，函数\(f\)是凸函数的充要条件是：\(f''(x) \ge 0\)。当\(\bf x\)是向量的时候，如果其hessian矩阵H是半正定的，\(H \ge 0\)，那么\(f\)是凸函数。如果\(f''(x)\)或者说\(H \gt 0\)，那么称\(f\)是严格凸函数。关于hessian矩阵是半正定的证明，可以参考知乎怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的？

Jensen不等式

Jensen是式2-1的泛化形式，或者说2-1是Jensen不等式的两点形式。

若对于任意点集\({x_i}\),若\(\lambda_i \ge 0\)且\(\sum_i \lambda_i=1\)，使用数学归纳法可以证明凸函数\(f(x)\)满足: \[ f\left(\sum_{i=1}^N\lambda_ix_i\right) \le \sum_{i=1}^N \lambda_if(x_i) \tag{2-2} \] 式2-2就称为Jensen不等式。

在概率论中，如果把\(\lambda_i\)看成取值为\(x_i\)的离散变量x的概率分布，那么公式2-2就可以写为： \[ f(E[x]) \le E[f(x)] \tag{2-3} \] 参考：如何理解Jensen不等式？ - 青崖白鹿记的回答 - 知乎

凹函数

凹函数和上面的凸函数结论是相反的，比如Jensen不等式则为： \[ \begin{align*} f\left(\sum_{i=1}^N\lambda_ix_i\right) &\ge \sum_{i=1}^N \lambda_if(x_i) \tag{2-4}\\ f(E[x]) &\ge E[f(x)] \tag{2-5} \end{align*} \]

EM算法

现在我们来讲解EM算法。

假设我们有N个独立的数据，\(\{x_1, \cdots x_N\}\)，我们想找到每个样本找到隐含的类别参数\(z\)，使得\(p(x,z)\)最大，其对数似然函数如下： \[ \begin{align*} l(\theta) &= \sum_{i=1}^N\log p(x_i ; \theta)\\ &=\sum_{i=1}^N \log \sum_{z_i} p(x_i,z_i ; \theta)\tag{3-1} \end{align*} \] 注意这里的符号：

写分号p(x; theta)表示待估参数（是固定的，只是当前未知）,应该可以直接认为是p(x)

from https://blog.csdn.net/pipisorry/article/details/42715245

前面提到过，由于隐变量\(z\)的存在，使得我们难以求解\(\theta\)。为此，EM的做法是不断的构造\(l(\theta)\)的下界(E-step)，然后优化下界(M-step)。

具体的做法是，对于每个样本i，令\(Q_i\)表示该样本隐含变量\(z\)的分布（比如上面的抛硬币案例，则指伯努利分布），\(Q_i\)满足\(\sum_z Q_i(z) = 1,\ Q_i(z) \ge 0\)。可得： \[ \begin{align*} l(\theta) = \sum_i \log p(x_i\mid \theta) &= \sum_i \log \sum_{z_i} p(x_i, z_iZ; \theta)\\ &= \sum_i \log \sum_{z_i} Q_i(z_i) \frac{p(x_i, z_i; \theta)}{Q_i(z_i)}\\ &\ge \sum_i \sum_{z_i}Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)} \tag{3-2} \end{align*} \] 最后一步是用Jensen不等式得到的， \[ \sum_{z_i} Q_i(z_i) \frac{p(x_i, z_i; \theta)}{Q_i(z_i)} \] 其实是\({p(x_i, z_i; \theta)}/{Q_i(z_i)}\)的期望，而\(\log\)函数是凹函数，根据Jensen不等式，有： \[ f\left(E_{z_i\sim Q_i}\left[\frac{ {p(x_i, z_i; \theta)} }{Q_i(z_i)}\right]\right) \ge E_{z_i \sim Q_i} \left[ f\left( \frac{ {p(x_i, z_i; \theta)} }{Q_i(z_i)} \right)\right] \] 这样，对于任意的分布\(Q_i\)，式3-2求得了\(l(\theta)\) 的下界，但是\(Q_i\)分布怎么选择呢？在很多种可能中如何选择最好的？假设已经知道了\(\theta\)，那么只需要最大化3-2，使得下界逼近\(l(\theta)\)即可。观察3-2，很容易发现，当3-2取等号的时候，说明下界达到了最大。而要取等号，根据Jensen不等式，需要让随机变量的值为常数，因此，我们有如下的约束： \[ \frac{p(x_i, z_i; \theta)}{Q_i(z_i)} = c \tag{3-3} \] 这里的c是一个不依赖于\(z_i\)的常数。我们继续进行推导，由于\(Q_i\)函数满足\(\sum_z Q_i(z) = 1\)，那么有\(\sum_z p(x_i, z_i; \theta) = \sum_z cQ_i(z_i) = c\)，带入3-3可得:

\[ \begin{align*} Q_i(z_i) &= \frac{p(x_i, z_i; \theta)}{\sum_z p(x_i, z_i; \theta)} \\ &= \frac{p(x_i, z_i; \theta)}{p(x_i;\theta)} \\ & = p(z_i \mid x_i;\theta) \tag{3-4} \end{align*} \] 于是得到\(Q_i\)就是后验概率分布\(p(z_i | x_i;\theta)\)。因此3-2的式子通过对数似然函数给定了\(l(\theta)\) 的下界，这个下界是我们想要去最大化的，这一步称为E步（E-step）。

接着是M步，最大化式3-2，也就是最大化\(l(\theta)\) 的下界（固定了\(Q_i(z_i)\)后，调整下界），于是得到EM算法的步骤为：

Random initialization \(\theta\) repeat until convergence { (E-step) For each i, set \(Q_i(z_i) = p(z_i \mid x_i; \theta)\) (M-step) Set \(\theta = \arg \max_\theta Q_i(z_i) = \sum_i \sum_{z_i}Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)}\) }

上面EM算法中，我们不断的进行E-step和M-step的迭代，直到收敛。那么，算法真的会收敛么？下面来证明一下。

收敛性证明

设\(\theta^{(t)}\)和\(\theta^{(t+1)}\)是第t轮和第t + 1轮迭代的结果，我们只需要证明\(l(\theta^{(t)}) \le l(\theta^{(t + 1)})\)就说明EM算法总是使得对数似然不断的增大，那么最终就会达到最大值。

根据3-2，有： \[ l(\theta^{(t)}) = \sum_i \sum_{z_i}Q_i^{(t)}(z_i) \log \frac{p(x_i, z_i; \theta^{(t)})}{Q_i^{(t)}(z_i)}\tag{3-5} \]

而参数\(\theta^{(t+1)}\)是通过最大化式3-5的，因此 \[ \begin{align*} l(\theta^{(t + 1)}) &\ge \sum_i \sum_{z_i}Q_i^{(t)}(z_i) \log \frac{p(x_i, z_i; \theta^{(t+1)})}{Q_i^{(t)}(z_i)}\tag{3-6} \\ &\ge \sum_i \sum_{z_i}Q_i^{(t)}(z_i) \log \frac{p(x_i, z_i; \theta^{(t)})}{Q_i^{(t)}(z_i)}\tag{3-7} \\ &=l(\theta^{(t)})\tag{3-8} \end{align*} \] 3-6的式子是因为式3-2，对于任意的分布\(Q_i\)，均有 \[ \begin{align*} l(\theta) &\ge \sum_i \sum_{z_i}Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)} \end{align*} \]

而3-7是因为我们M-step后，得到的\(\theta^{(t+1)}\)采用的是: \[ \arg \max_\theta \sum_i \sum_{z_i}Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)} \] 因此，有3-7成立，而3-8就是式子3-5。

如果定义 \[ g(Q, \theta) = \sum_{z_i}Q_i(z_i) \log \frac{p(x_i, z_i; \theta)}{Q_i(z_i)}\tag{3-9} \] 我们知道有\(l(\theta) \ge g(Q, \theta)\)。EM算法可以理解为对\(g(Q, \theta)\)运用坐标轴上升法，E-step固定\(\theta\)来优化\(Q\)，使得下界g在\(\theta\)处与\(l(\theta)\)相等，而M-step固定\(Q\)来优化\(\theta\)，求使得下界\(g(Q, \theta)\)达到最大值的\(\theta\)，从而使得\(l(\theta)\)的值也变大。下图直观的反应了这一过程。

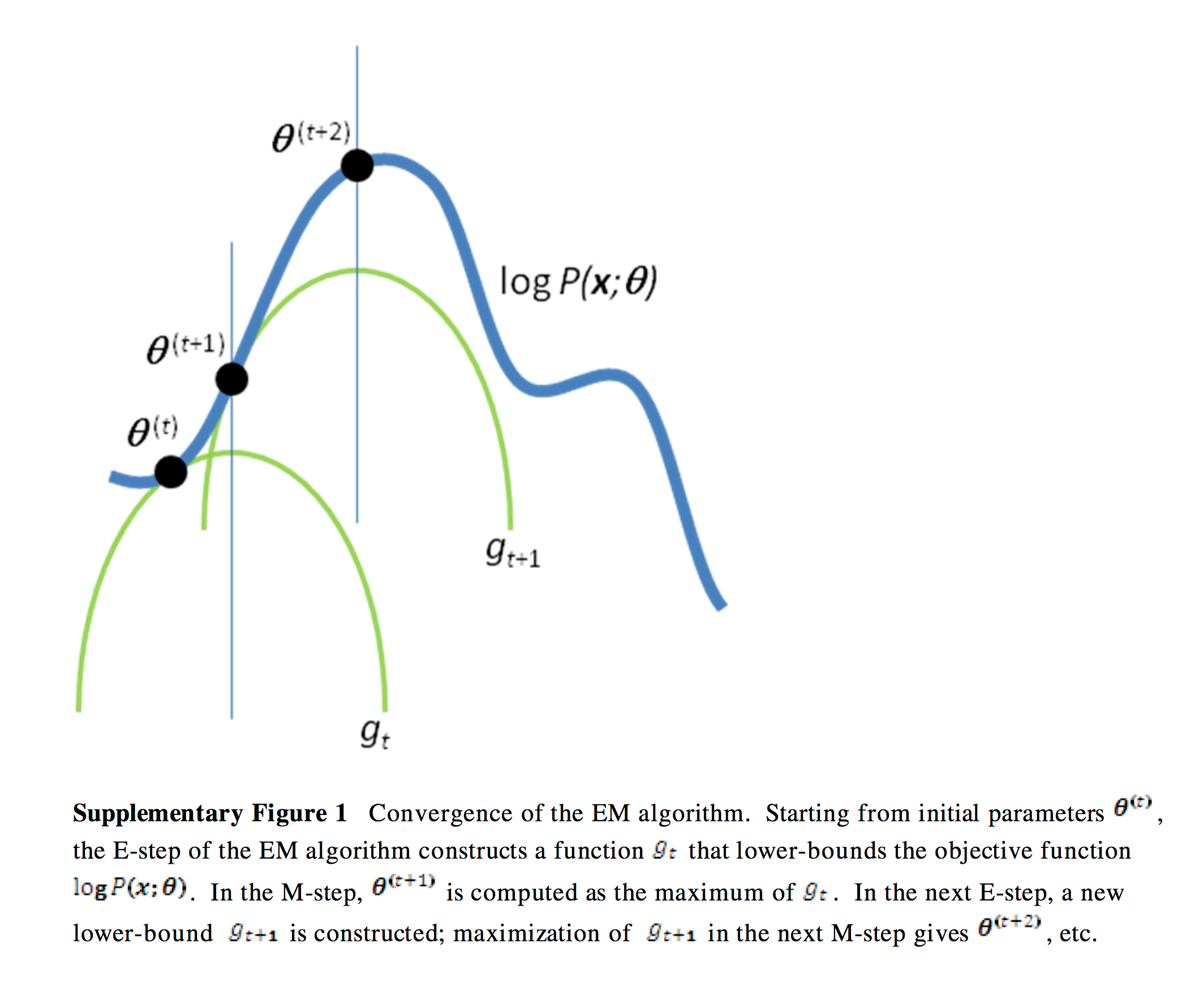
回顾硬币例子

在前面的硬币例子中，我们首先做的是随机初始化概率\(\hat P_A, \hat P_B\)。

然后是E-step：估计后验概率\(P({\bf z_i} \mid x_i)\)，这里的隐变量\(z_i = \{z_{iA}, z_{iB} \}\)。可以理解为若\(z_{iA} = 1\)则说明第i个样本为硬币A产生，若\(z_{iB}=1\)则说明第i个样本为硬币B产生。分别计算硬币可能由A和B的似然值a和b，然后计算\(P(z_{iA}=1\mid x_i) = a_i / (a_i+ b_i)\)和\(\ P(z_{iB} = 1\mid x_i) = b_i / (a_i+ b_i)\)。

接着是M-step：根据每个样本估计出是属于哪一个硬币的结果\(z_{iA}\)和\(z_{iB}\)，计算出新的概率\(P_A, P_B\)

EM算法最优解

EM算法不能保证找到全局最优解，只能保证收敛到对数似然函数的稳定点，不能保证收敛到极大值点。所以在应用中初始值的选择十分重要，常用的办法是选取几个不同的初值进行迭代，然后对得到的各个估计值加以比较，从中选择最好的。

参考资料

[1] Do C B, Batzoglou S. What is the expectation maximization algorithm?[J]. Nature biotechnology, 2008, 26(8): 897. [2] The EM algorithm， CS229 Lecture notes Part IX [3] （EM算法）The EM Algorithm