本文介绍:
- 线性回归
- 逻辑回归
- Softmax
- 并行化逻辑回归
线性回归
回归问题举个简单的例子,如预测股票的价格,输出空间y不再是一个标签,而是一个实数集。
对此,线性回归问题的假设是: \[ f({\bf x}) = {\bf w^T x} + b \]
可以看出和感知机的模型很像,只不过不用取sign,因为最后结果就是个连续的值。
有时为了方便表示,将b吸收进w,而把所有的样本x添加一列为1,成为一个矩阵X: \[ {\bf w} = ({\bf w_{old} },b) \]
\[ \rm X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nd} & 1 \\ \end{bmatrix} \]
于是得到: \[ f({\bf x}) = \rm X{\bf w} \]
设样本数为n,特征数为d,则维度为:
- \(\rm X\): n * (d + 1)
- \({\bf y}\): n * 1
- \({\bf w}\): (d + 1) * 1
优化目标
在回归问题中,均方误差是常见的性能度量,公式如下: \[ {\rm err}(f({\bf x}), y) = (f({\bf x}) - y)^2 \] 均方误差对应了常见的欧几里得距离,基于均方误差最小化来进行模型求解的方法称为最小二乘法。
线性回归便是用均方误差作为损失函数, \[ \begin{align*} L({\bf w}) & = (f({\bf x}) - {\bf y})^2 \\ & = (\rm X{\bf w} - {\bf y})^T (\rm X{\bf w} - {\bf y}) \end{align*} \] 其实也就是找一个w使得损失函数最小:
\[ {\bf w}^* = \rm{arg min_{\bf w} } (X{\bf w} - {\bf y})^T (X{\bf w} - {\bf y}) \]
求解
对w求导得: \[ \frac{\partial L({\bf w})}{\partial {\bf w} } = 2\rm X^T(\rm X{\bf w} - {\bf y}) \] 若\(\rm X^TX\)是可逆的,令导数为0便得到: \[ {\bf w}^* = ({\rm X^TX})^{-1}{\rm X^T}{\bf y} \]
通常有特征数d << 样本数m,使得\(\rm X^TX\)满秩,有唯一解。
但是也有许多情况m < d,这样\(\rm X^TX\)不是满秩的,会有多组解。此时可以解出多个w,都能使均方误差最小化。选择哪一解作为输出将由学习算法归纳偏好决定。
实际求解过程中,一般都直接求解\(\rm (X^TX)^{−1}X^T\) ,\(\rm (X^TX)^{−1}X^T\)称为\(\rm X\)的伪逆,记作\({\rm X}^\dagger\)。
求解出伪逆后,线性回归模型为: \[ f({\bf x}) = \rm X (X^\dagger {\bf y}) \]
空间变换
线性回归可以进行输出空间的变换。
比如当我们觉得样本的是在指数尺度上变化,我们可以加个指数的变换使得\(f({\bf x})\)接近y \[ f({\bf x}) = e^{ {\bf w^Tx}+b} \] 也就是求解: \[ \ln y = {\bf w^T x }+b \] 便得到了对数线性回归,如图(图来自周志华的《机器学习》):
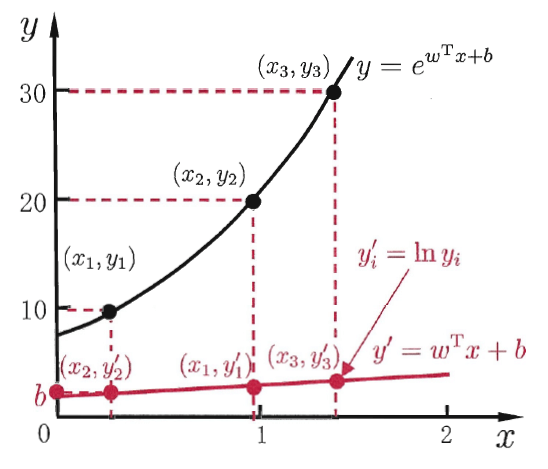
这里对数函数起到了将线性回归模型的预测值与真实值联系起来的作用。
更一般的,考虑单调可谓函数g,令: \[ y = g^{-1}({\bf w^Tx}+b) \] 这样的模型称为”广义线性模型“。g称为联系函数,显然对数线性回归是g = ln时的特例。
逻辑回归
现在来讲讲逻辑回归(Logistic Regression),虽然它的名字叫“回归”,但其实它用于分类任务。
在二分类问题中,我们的训练数据集是 \(T = \{(x_1,y_1), \cdots,(x_n,y_n)\}\) ,其中\(y_i \in \{-1, +1\}\)。训练数据的标签是-1和+1,那么我们预测也是输出+1或者-1标签。但是有时候我们想知道的是概率,即为正例或负例的概率是多少。比如用于医院的任务中,给定一个病人,预测其是否得某种病a。不仅是关心ta是否得病,还关心得病的概率是多少。这个问题与原来的二分类问题有所差别,被称作“软二元分类”问题。求解此问题得到的值越高,说明越有可能是得病a的,否则越有可能是不得病a的。此时目标函数会变化成\(f({\bf x})=P(+1|{\bf x})∈[0,1]\)的形式
和之前一样,我们仍可以假设计算加权分数,即 \[ z = \sum_{j=0}^d w_jx_j = {\bf w^Tx} \] 然后,将该分数缩放到[0, 1]这个区间。而缩放操作通常使用Logistic函数来完成,因此这个问题称为Logistic回归问题,假设也被称为Logistic假设。
Logistic函数与逻辑回归模型
现在介绍神奇的Logistic函数 \[ \sigma(z)= \frac{e^{\bf z} }{1+e^{\bf z} } = \frac{1}{1+e^{-{\bf z} }} \] 画出二维的图:
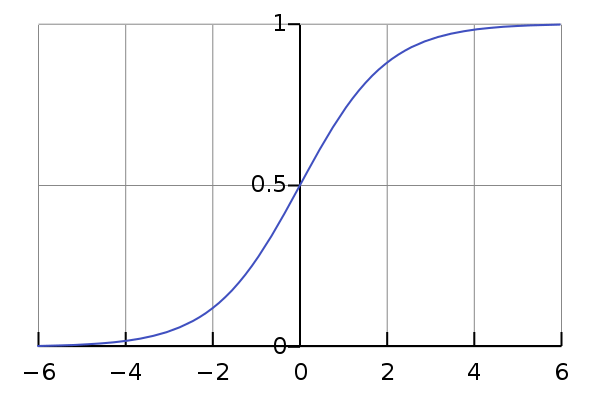
从上图可以看出,对数几率函数是一种Sigmoid函数(即形似s的函数),它将z值转化为接近0或1的y值。
将上面的假设带入Logistic函数,便得到我们的逻辑回归模型,这里设为\(h({\bf x})\) : \[ h({\bf x}) = \sigma({\bf w^Tx}) = \frac{1}{1+e^{-({\bf w^Tx})} } \tag{2-1} \] 按照上面的说法,我们进行了”映射“,这就是输出为正例的概率,因此 \[ \begin{align} p(Y = 1 | {\bf x}) &= h({\bf x}) = \frac{1}{1+e^{-{\bf w^Tx} }} \\ p(Y = 0 | {\bf x}) &= 1-P(Y = 1|{\bf x}) \\ &= \frac{1}{1+e^{ {\bf w^Tx} }} \\ \end{align} \] 现在可以讨论Logistic函数的特点了,一个事件的几率(odds) 是该事件发生的概率与该事件不发生概率的比值,如果事件发生的概率为p,那么该事件的几率是\(\frac{p}{1-p}\),该事件的对数几率(就是取对数)是: \[ \ln \frac{p}{1-p} \] 对于逻辑回归而言: \[ \ln \frac{P(Y = 1|{\bf x}) }{1-P(Y = 1|{\bf x}) } = \ln \frac{\frac{e^{\bf w^Tx} }{1+e^{\bf w^Tx} }}{\frac{1}{1+e^{\bf w^Tx} }} = {\bf w^Tx} \] 因此可以看出,实际上我们的逻辑回归模型是用线性回归模型的预测结果去逼近真实标记的对数几率。
因此,我们用Logistic函数,并使用了线性函数\(\bf w^Tx\)完成了实数域到输出区间[0,1](概率值)的转化。
参数估计与损失函数
那么,如何确定逻辑回归模型中的w呢?我们可以使用极大似然法(maximum likelihood method)估计模型参数w。
写出似然函数为: \[ \prod_{i=1}^N h({\bf x_i})^{y_i} (1- h({\bf x_i}))^{1-y_i}\\ \] 取对数似然为: \[ \sum_{i=1}^N [y_i\ln h({\bf x_i}) + (1-y_i)\ln(1- h({\bf x_i}))] \]
求上式的最大值即可得到w的估计值。但实际中,我们一般喜欢优化极小值,因此取个负号,得到我们逻辑回归的损失函数: \[ L(w) = -\sum_{i=1}^N [y_i\ln h({\bf x_i}) + (1-y_i)\ln(1- h({\bf x_i}))]\tag{2-2} \]
梯度下降求解
式2-2给出了损失函数L(w),该函数是关于w的高阶可导连续凸函数,可以用梯度下降法、牛顿法求解。
下面使用最常用的梯度下降法。
为了方便的求解偏导,首先计算sigmoid函数的导数\(\sigma(z) = \frac{1}{1+e^{-z} }\)的偏导: \[ \begin{align*} \frac{\partial \sigma}{\partial z} &= -\left(\frac{1}{1+e^{-z} }\right)^2 \frac{\partial e^{-z} }{\partial z}\\ &= -\left(\frac{1}{1+e^{-z} }\right)^2 e^{-z} (-1)\\ &= \sigma(z) \left(\frac{ e^{-z} }{1+e^{-z} }\right) \\ &=\sigma(z)(1 - \sigma(z)) \end{align*} \] 对于\(h({\bf x_i})\)对\(w_j\)的偏导则为: \[ \begin{align*} \frac{\partial h({\bf x_i})}{\partial w_j} &= -\left(\frac{1}{1+e^{-z} }\right)^2 \frac{\partial e^{-z} }{\partial z}\frac{\partial z}{\partial w_j}\\ &=\sigma(z)(1 - \sigma(z)) x_{ij} \\ &= h({\bf x_i})(1-h({\bf x_i}))x_{ij} \end{align*} \] 求完前面,现在可以容易求L(w)对\(w_j\)求偏导啦: \[ \begin{align*} \frac{\partial L(\bf w)}{\partial w_j} &= -\sum_{i=1}^N [y_i(1-h({\bf x_i}))x_{ij} - (1-y_i)h({\bf x_i})x_{ij}]\\ &= \sum_{i=1}^N[-y_ix_{ij} + h({\bf x_i})x_{ij}] \\ &= \sum_{i=1}^N \left(h({\bf x_i}) -y_i \right)x_{ij} \end{align*} \] 于是,w的更新公式为: \[ w_j = w_j - \eta\sum_{i=1}^N(h({\bf x_i}) -y_i )x_{ij}\tag{2-3} \]
注意上述的更新公式有连加符号,在python的实现中,如果用for是非常慢的,我们希望能向量化上述式子,从而使用Numpy来加速过程。
查了半天资料,基本没个详细的,自己推吧。
那么,怎么加速呢?
分析公式2-3,我们发现\(w_j\)更新是\(w_j\)减去步长 乘上 每个训练数据的\(h({\bf x_i})-y_i\)并乘上对应的\(\bf x_i\)的j维。
如何消去累加? 联想到向量乘法或者矩阵乘法就是有累加的过程!
本文最开始的时候讲过:
\[ \rm X = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nd} & 1 \\ \end{bmatrix} \]
维度如下:
- X: N * (d + 1)
- \({\bf y}\): N * 1
- \({\bf w}\): (d + 1) * 1
我们可以构造矩阵 \[ \begin{align} X^T(h(x) - y) &= \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nd} & 1 \\ \end{bmatrix} ^T \begin{bmatrix}h(x_1) - y_1 \\h(x_2) - y_2 \\ \vdots \\h(x_n) - y_n \\\end{bmatrix} \\& = \begin{bmatrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1d} & x_{2d} & \cdots & x_{nd} \\ 1 & 1 & \cdots &1 \\ \end{bmatrix} \begin{bmatrix}h(x_1) - y_1 \\h(x_2) - y_2 \\ \vdots \\h(x_n) - y_n \\\end{bmatrix} \\&= \begin{bmatrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1d} & x_{2d} & \cdots & x_{nd} \\ x_{1(d+1)} & x_{2(d+1)} & \cdots & x_{n(d+1)} \\ \end{bmatrix} \begin{bmatrix}h(x_1) - y_1 \\h(x_2) - y_2 \\ \vdots \\h(x_n) - y_n \\\end{bmatrix} \\&= \begin{bmatrix} \sum_{i=1}^n(h(x_i)-y_i) x_{i1} \\ \sum_{i=1}^n(h(x_i)-y_i) x_{i2} \\ \vdots \\ \sum_{i=1}^n(h(x_i)-y_i) x_{id} \\ \sum_{i=1}^n(h(x_i)-y_i) x_{i(d+1)} \\ \end{bmatrix} \end{align} \] 推导到这很明显了吧?
还不明显,那么继续: \[ \begin{align} {\bf w} &= {\bf w}- \eta {\rm X^T}(h({\bf x}) - {\bf y}) \\& = \begin{bmatrix} w_1 \\ w_2 \\ \vdots\\ w_d\\ w_{d+1} \end{bmatrix}-\eta \begin{bmatrix} \sum_{i=1}^n(h(x_i)-y_i) x_{i1} \\ \sum_{i=1}^n(h(x_i)-y_i) x_{i2} \\ \vdots \\ \sum_{i=1}^n(h(x_i)-y_i) x_{id} \\ \sum_{i=1}^n(h(x_i)-y_i) x_{i(d+1)} \\ \end{bmatrix} \\& = \begin{bmatrix} w_1 - \eta\sum_{i=1}^n(h(x_i)-y_i) x_{i1} \\ w_2- \eta\sum_{i=1}^n(h(x_i)-y_i) x_{i2} \\ \vdots \\ w_d - \eta\sum_{i=1}^n(h(x_i)-y_i) x_{id} \\ w_{d+1} - \eta \sum_{i=1}^n(h(x_i)-y_i) x_{i(d+1)} \\ \end{bmatrix} \tag{2-4} \end{align} \] 看到这里就懂了吧? 式2-4是2-3等价的矩阵表示。
因此我们可以用式2-4来写程序~
这也是《机器学习实战》中倒数第二行式子的由来:
1 | def gradAscent(dataMatIn, classLabels): |
另一种似然函数
在上面推导损失函数2-2的时候,我们y的标签为{0,1},如果我们我们假设标签为{-1, +1},那么同样用极大似然估计,会得到很多材料上的另一种类似的似然函数。
推导如下: \[ \begin{align} p(Y = +1 | {\bf x}) &= h({\bf x}) = \frac{1}{1+e^{-{\bf w^Tx} }} \\ p(Y = -1 | {\bf x}) &= 1-P(Y = 1|{\bf x}) \\ &= \frac{1}{1+e^{ {\bf w^Tx} }} \end{align} \] 由于sigmoid有性质\(h(-x) = 1 - h(x)\),因此上面两式可以合并为: \[ p(y |{\bf x}) = h(y{\bf x}) = \frac{1}{1+e^{-y{\bf w^Tx} }} \] 写出似然函数为: \[ \begin{align*} \prod_{i=1}^n p(y_i |{\bf x_i}) &= \prod_{i=1}^n h(y_i{\bf x_i}) \\ &=\prod_{i=1}^n\frac{1}{1+e^{-y_i{\bf w^Tx_i} }} \end{align*} \] 取对数似然有: \[ \sum_{i=1}^n \ln\frac{1}{1+e^{-y_i{\bf w^Tx_i} }} = -\sum_{i=1}^n \ln(1+e^{-y_i{\bf w^Tx_i} }) \] 取负值就得到另一种损失函数 \[ L(w) =\sum_{i=1}^n\ln(1+e^{-y_i{\bf w^Tx_i} })\tag{2-5} \]
Softmax
逻辑回归是处理二分类的问题,我们可以将它推广到多分类的情况,就是Softmax: \[ h({\bf x}) = \left[ \begin{aligned}z_1 \\z_2 \\ ...\\z_K \end{aligned}\right]=\frac{1}{\sum_{j=1}^Ke^{\bf w_j^Tx} }\left[ \begin{aligned}e^{\bf w_1^Tx} \\e^{\bf w_2^Tx} \\ ...\\e^{\bf w_K^Tx} \end{aligned}\right]\tag{3-1} \] 看上去仿佛很复杂,因为它输出的是一个向量,向量中每一项分别表示对应类别的概率。而对于每个类别都有一个\(w_k\)
假如说求解第k个类别的概率,那么输出就是一个实数: \[ P(y=k|\ {\bf x,w}) = h_k({\bf x}) =\frac{e^{\bf w_k^Tx} }{\sum_{j=1}^Ke^{\bf w_j^Tx} }\tag{3-2} \]
这里的数据集形式为:\(\{ {(\bf x_1, y_1}), ({\bf x_2, y_2}), \cdots, ({\bf x_N, y_N}) \}\)
这里\(\bf x\)是一个D * 1的向量(D为特征数)。而\({\bf y_i}\)则是一个只有一个数字为1,其余都是0的K * 1维向量,用来表示这个样本属于哪个类别。
Softmax学习
和逻辑回归一样,采用极大似然估计。对于单个服从多项分布的单个样本,其似然函数为: \[ \prod_{k=1}^K h_k^{y_k},\\ 其中,h_k = h_k({\bf x})=\frac{e^{\bf w_k^Tx} }{\sum_{j=1}^Ke^{\bf w_j^Tx} } \] 老样子,我们采用对数似然,并取相反数得:
\[ L({\bf W}) = -\sum_{k=1}^K y_k\ln h_k\tag{3-3} \] 3-3也被称为交叉熵损失(cross entropy loss)。注意这里的符号是大写加粗的\(\bf W\),表示为一个矩阵,形式为\(\bf [w_1, w_2,\cdots,w_K]\),每个类别都有一个d维的参数\(w_k\),合起来就是d * K。
要优化3-2,可以用梯度下降的方法进行求导。
为了简单起见,我们先让\(h_k\)对\(\bf w_j\)求偏导,求导需要注意有\(j=k\)和\(j \ne k\)两种情况,需要分开计算。
对于\(j=k\)的情况,有: \[ \begin{align*} \frac{\partial h_k}{\partial \bf w_j} &= \frac{e^{\bf w_k^Tx} }{\sum_{a=1}^Ke^{\bf w_a^Tx} } {\bf x} - \frac{e^{\bf w_k^Tx} }{(\sum_{a=1}^Ke^{\bf w_a^Tx})^2} e^{\bf w_j^Tx} {\bf x}\\ &=h_k (1 - h_j){\bf x} \\ &=h_j (1 - h_j){\bf x} \tag{3-4} \end{align*} \] 对于\(j \ne k\)的求导,有: \[ \begin{align*} \frac{\partial h_k}{\partial \bf w_j} &= - \frac{e^{\bf w_k^Tx} }{(\sum_{a=1}^Ke^{\bf w_a^Tx})^2} e^{\bf w_j^Tx} {\bf x}\\ &=-h_k h_j{\bf x}\tag{3-5} \end{align*} \] 于是,我们现在就可以求3-3 单个样本的交叉熵的导数了: \[ \begin{align*} \frac{\partial L({\bf W})}{\partial \bf w_j} & = -\sum_{k} y_k \frac{\partial \log h_k}{\partial \bf w_j}\\ &= -\sum_{k} y_k \frac{1}{h_k}\frac{\partial h_k}{\partial \bf w_j}\\ &= -y_j \frac{1}{h_j}h_j (1 - h_j){\bf x} + \sum_{k\ne j}y_k \frac{1}{h_k}h_kh_j{\bf x}\\ &=- y_j (1 - h_j){\bf x} + \sum_{k\ne j}y_k h_j{\bf x}\\ &= \left(-y_j +y_jh_j+ \sum_{k\ne j}y_kh_j\right) {\bf x}\\ &= \left(-y_j +\sum_{k}y_kh_j\right) {\bf x} \\ &= \left(-y_j +h_j\sum_{k}y_k\right) {\bf x} \\ &= \left(h_j -y_j\right) {\bf x} \\ \end{align*} \] 进一步的,如果要计算整个训练集的损失,可以求: \[ L({\bf W}) = -\sum_{i=1}^N\sum_{i=1}^K y_k\ln h_k({\bf x_i})\tag{3-4} \]
参数的冗余性
Softmax 回归有一个不寻常的特点:它有一个“冗余”的参数集。 比如说,我们对每个类别参数\(\bf w_k\)都减去一个向量\(\theta\),得: \[ \begin{align*} P(y=k|\ {\bf x,w}) = h_k({\bf x}) &=\frac{e^{\bf (w_k - \theta)^Tx} }{\sum_{j=1}^Ke^{\bf (w_j- \theta)^Tx} }\\ &=\frac{e^{\bf w_k ^Tx} e^{\bf - \theta^Tx} }{\sum_{j=1}^Ke^{\bf w_j^Tx}e^{\bf - \theta^Tx} }\\ &=\frac{e^{\bf w_k^Tx} }{\sum_{j=1}^Ke^{\bf w_j^Tx} } \end{align*} \] 可以看到减去一个向量完全不影响预测结果!这说明如果参数\(\bf (w_1, w_2,\cdots , w_k)\)是已经根据损失函数求解后的极小值点,那么\(\bf (w_1 - \theta, w_2 - \theta,\cdots , w_k - \theta)\)同样也是极小值点。因此解不唯一。
解决这个问题可以加入权重衰减(weight decay),说白了就是加入L2正则项。
3-4就变为: \[ L({\bf W}) = -\sum_{i=1}^N\sum_{k=1}^K y_k\ln h_k({\bf x_i}) + \sum_{i=1}^d \sum_{k=1}^Kw_{ij}^2 \tag{3-4} \]
和逻辑回归的关系
当k = 2时,Softmax表达式为: \[ h({\bf x}) = \frac{1}{e^{\bf w_1^Tx}+e^{\bf w_2^Tx} }\left[ \begin{aligned}e^{\bf w_1^Tx} \\e^{\bf w_2^Tx} \end{aligned}\right] \] 利用冗余性的特点,参数都减去\(w_1\),得: \[ \begin{align*} h({\bf x}) &= \frac{1}{e^{\bf (w_1 - w_1)^Tx}+e^{\bf (w_2 - w_1)^Tx} }\left[ \begin{aligned}e^{\bf (w_1 - w_1)^Tx} \\e^{\bf (w_2 - w_1)^Tx} \end{aligned}\right]\\ &= \frac{1}{1+e^{\bf (w_2 - w_1)^Tx} }\left[ \begin{aligned} 1 \\e^{\bf (w_2 - w_1)^Tx} \end{aligned}\right] \\ &= \left[ \begin{aligned} \frac{1}{1+e^{\bf (w_2 - w_1)^Tx} } \\ \frac{e^{\bf (w_2 - w_1)^Tx} }{1+e^{\bf (w_2 - w_1)^Tx} } \end{aligned}\right] \\ &= \left[ \begin{aligned} \frac{1}{1+e^{\bf (w_2 - w_1)^Tx} } \\ 1 -\frac{1}{1+e^{\bf (w_2 - w_1)^Tx} } \end{aligned}\right] \\ \end{align*} \] 令\(\bf w = w_2 - w_1\),得一个类别的概率为\(\frac{1}{1+e^{\bf w^Tx} }\),另一个类别的概率为\(1 - \frac{1}{1+e^{\bf w^Tx} }\),这和逻辑回归是一样的。
因此,可以说Softmax是Logistic 回归的一般形式,当K=2时,Softmax退化为logistic回归。
使用Softmax 还是K个逻辑回归
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 Softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
如果你的类别是互斥的,那么用Softmax,否则用K个逻辑回归:
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的Softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
如果你的四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的 logistic 回归分类器更为合适。这样,对于每个新的音乐作品,我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子,你的任务是将图像分到三个不同类别中。
- 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。你会使用Softmax回归还是 3个logistic 回归分类器呢?
- 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,你又会选择 Softmax回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择Softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。
并行化逻辑回归
逻辑回归虽然简单,但是在真实环境中,数据量大,也往往对其做并行化处理。
这里,我们首先要复习一下逻辑回归的更新公式2-3: \[ w_j = w_j - \eta\sum_{i=1}^N(h({\bf x_i}) -y_i )x_{ij}\\ 其中,h({\bf x_i}) = \frac{1}{1+e^{-({\bf w^Tx_i})} } \] 注意到\(\bf w\)的维度为d,需要对数据的每一维都使用上式更新。可以看到,一次更新的开销数据量N以及维度d有关。
数据并行
这是最简单也是最容易想到的数据并行方式了,假设有a台机器,则把数据随机分到a台机器上,每台机器数据不重复,这样每台机器有N/a条样本,每个样本有d个特征。每台机器分别对其样本计算\((h({\bf x_i}) -y_i )x_{ij}\),最后求和合并即可。
这个方式解决了数据量大的问题,但是实际中特征数量可能很高。
特征并行
特征并行就是对特征进行划分,假设有b台机器,那么,每台机器的有\(\frac{d}{b}\)个特征,N个样本,每台机器对其拥有的特征j分别计算\((h({\bf x_i}) -y_i )x_{ij}\),然后和其它机器同步更新后的参数即可。
数据+特征并行
数据+特征并行就是上面两种的结合,如下图所示,将数据分为a * b块,其中,即将数据按水平划分,又在特征上垂直划分。
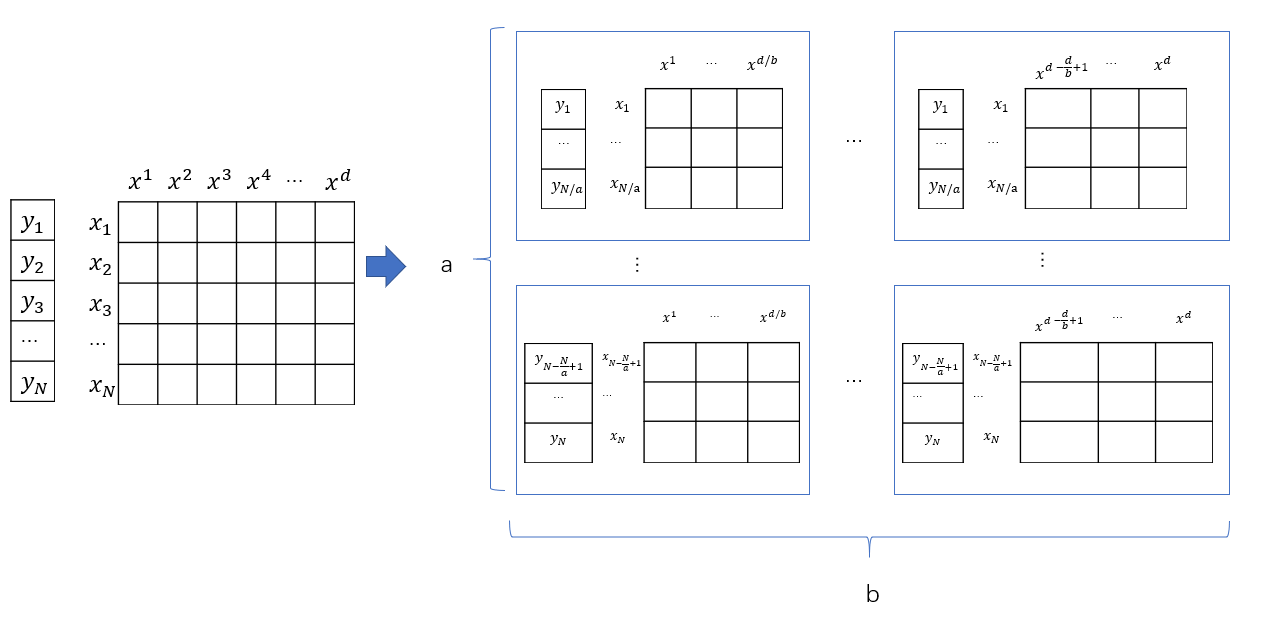
看看公式2-3,我们需要计算\(\bf w^Tx\),因此,我们可以对所有机器分别计算\(\sum_{j} w_jx_{ij}\),然后按照行号相同的进行归并,就得到了\(\bf w^Tx_i\)。
此外,我们需要计算\(\sum_{i=1}^N(h({\bf x_i}) -y_i )x_{ij}\),这就是要让列号相同的结点进行归并。
Google DistBelief
Google实现了一个名为DistBelief的框架,采用parameter server来同步参数,如下图:
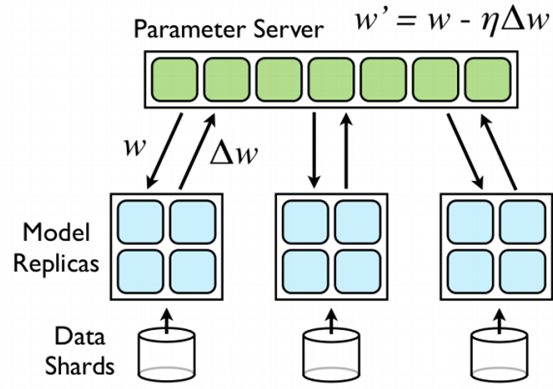
将训练数据划分为若干个子集,并在每一个子集上运行一个单独的模型副本,各模型副本通过参数服务器来交换梯度信息,参数服务器用来维护模型参数当前的状态,它也分布在多台机器上(假如有10台机器,那么每台机器将负责存储和更新1/10的模型参数,因此,每个模型副本只需要和parameters中和该结点有关的模型参数那部分结点进行通信)。
可以看出,这里面有两种异步性:
- 模型副本之间的运行是独立的
- 参数服务器之间的机器也是独立的
如果每个模型副本处理完一个样本就和参数服务器进行通信,那么通信量会很大,为了减少通信的开销,设置了两个参数:\(n_{fetch}\)和\(n_{push}\),每\(n_{fetch}\)向服务器取一次参数,每\(n_{push}\)次向服务器推送结果,\(n_{fetch}\)不一定等于\(n_{push}\)
此外,
- 一个Model replicas失效并不影响其它的Model replicas,因此鲁棒性很强
- Model replicas是异步执行的,省去了同步时间
- 每个 Model Replicas 中的 fetch compute push 操作是通过三个线程完成的,类似于流水线机制,大大加快了速度
- 参数服务器的每个节点更新参数的次数不一定相同,有一定的随机性
然而,这样的异步处理方式使得模型具有很大的随机性,主要体现在一个模型计算样本的梯度的时候,采用的是一组稍微过时的参数,因为它在计算梯度时,其它副本很可能已经对参数服务器中的参数进行了更新;并且某一个时刻,各个机器上的参数更新次数和更新顺序不一定相同。这样的做法缺乏理论基础,但最后得到的模型效果还是不错的。
参考资料
- 《机器学习》 周志华
- 《统计学习方法》 - 李航
- 机器学习基石 - 林轩田
- 机器学习--Logistic回归计算过程的推导
- http://blog.csdn.net/ligang_csdn/article/details/53838743
- http://blog.csdn.net/jediael_lu/article/details/77852060
- Softmax
https://deepnotes.io/softmax-crossentropy
- 并行化逻辑回归

