『我爱机器学习』集成学习（二）Boosting与GBDT

在上一章节中，我们介绍了模型融合以及Bagging方法，本文主要介绍Boosting相关方法。包括：

• Boosting
• Adaboost
• GBDT

Boosting

Boosting也叫提升法，是一类将弱学习器提升为强学习器的算法。

这类算法的工作机制类似：先从初始训练集中训练出一个基学习器，再根据学习器的表现对训练样本分布进行调整，使得先前基学习器做错的样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直到基学习器数目达到事先指定的T，最终将T个基学习器进行加权结合。

Adaboost

首先给出Adaboost的算法：

输入: 训练集 \(Data =\{({\bf x_1},y_1),({\bf x_2},y_2),\cdots,({\bf x_N},y_N)\}, y_i \in\{+1, -1\}\);

​ 训练轮数T，

​ 训练算法G

过程：

​ 初始化样本权重 \(D_{1,i} = \frac{1}{N}, i=1,2,\cdots,N\)

​ for t = 1 to T do

​ \(h_t = G({\rm Data} , D_t)\) # 用训练算法G基于权重\(D_t\)训练出当前的分类器\(h_t\)

​ \(\epsilon_t = \sum_{i=1}^N D_{t,i}I(h_t(x_i) \ne y_i)\) # 计算误差

​ if \(\epsilon_t > 0.5\) then break

​ \(\alpha_t = \frac{1}{2}\ln(\frac{1 - \epsilon_t }{\epsilon_t})\) #计算分类器\(h_t\)的权重

​ \(D_{t+1,i} = \frac{1}{Z_t}\left( D_{t,i} \cdot exp(-y_i\alpha_th_t({\bf x_i}))\right)\) # 更新样本权重，其中，归一化因子：\(Z_t = {\sum_{i=1}^N D_{t,i}}\cdot exp\left(-y_i\alpha_th_t({\bf x_i}) \right)\)

输出：

​ \(H({\bf x}) = sign(\sum_{t=1}^T \alpha_t h_t({\bf x}))\)

一张直观的图如下：

adboost

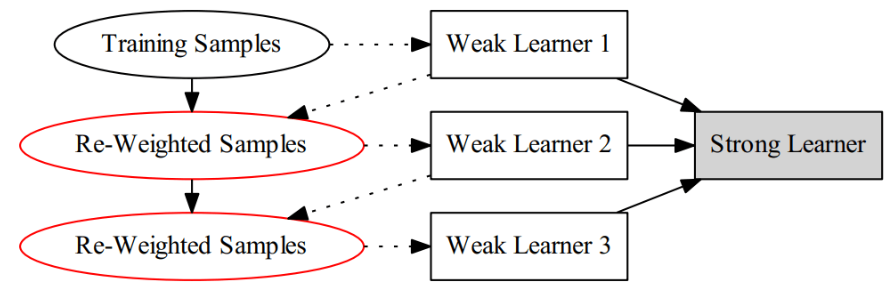
描述起来好像很容易的样子：

• 初始化每个样本权值均等，都为1 / N
• 然后迭代T轮，在每一轮中学习中根据错误率\(\epsilon_t\)改变训练数据的权值分布，增加分类错误的权重，减少分类正确的样本权重。这样，新一轮的学习中将会更加重视对之前分错的样本。
• 将T轮得到的T个分类器\(h_t({\bf x})\)和对应的分类器权重\(\alpha_t\)进行线性组合，就得到最终结果\(H({\bf x}) = sign(\sum_{t=1}^T \alpha_t h_t({\bf x}))\)

注意到当错误率\(\epsilon \gt 0.5\)的时候，我们不再计算。因为对于二分类问题，错误率大于一半意味着不如随机乱猜，留之无用。

Adaboost模型让人困惑的地方有两个：

1. 分类器权重\(\alpha_t\)为啥等于\(\frac{1}{2}ln(\frac{1 - \epsilon_t }{\epsilon_t})\)
2. 样本权重公式和归一化因子是怎么来的？

分类器权重的由来

Adaboost的分类器权重公式为：\(\alpha_t = \frac{1}{2}ln(\frac{1 - \epsilon_t }{\epsilon_t})\) ，这是怎么来的呢？

可以从最小化训练误差界来推导，也可以从最小化损失函数进行推导。这两种本质上是一样的，都是极小化某式得到的\(\alpha_t\)。

这里采用最小化训练误差界来推导。

训练误差界

Adaboost的训练误差界为： \[ \frac{1}{N}\sum_{i=1}^N I \left(H({\bf x_i}) \ne y_i \right) \le \frac{1}{N}\sum_{i=1}^N exp(-y_if({\bf x_i})) = \prod_{t}Z_t \tag{2-1} \] 其中\(f({\bf x}) = \sum_t \alpha_th_t({\bf x})； H({\bf x}) = \rm sign(f({\bf x}))\)

好像很复杂，我们先来不管最后那个等式，只看前面的不等式，就是说指数损失是0-1损失函数的上界。这个很好证明，当\(H({\bf x_i}) \ne y_i\)时，\(-y_if({\bf x_i})< 0 \Rightarrow exp(-y_if({\bf x_i})) \ge 1\)。

在证明右边的等式之前，我们先回顾一下权重的定义： \[ \begin{align*} & D_{t+1,i} = \frac{D_{t,i}}{Z_t}\cdot \exp(-y_i\alpha_th_t({\bf x_i})) \\ \Rightarrow \ & Z_tD_{t+1,i} = D_{t,i}\cdot \exp(-y_i\alpha_th_t({\bf x_i})) \tag{2-2} \end{align*} \] 现推导如下： \[ \begin{align*} \frac{1}{N}\sum_{i=1}^N \exp(-y_if({\bf x_i})) &= \frac{1}{N}\sum_{i=1}^N \exp\left (\sum_{t=1}^T-y_i\alpha_th_t({\bf x})\right) \\& =\sum_{i=1}^N D_{1,i} \prod_{t=1}^{T} \exp\left (-y_i\alpha_th_t({\bf x})\right) \hspace{5ex} D_{1,i}= \frac{1}{N} \\& =Z_1\sum_{i=1}^N D_{2,i} \prod_{t=2}^{T} \exp\left (-y_i\alpha_th_t({\bf x})\right) \hspace{5ex} 式2-2 \\& =Z_1Z_2\sum_{i=1}^N D_{3,i} \prod_{t=3}^{T} \exp\left (-y_i\alpha_th_t({\bf x})\right) \\& =Z_1Z_2\cdots Z_{T-1}\sum_{i=1}^N D_{T,i} \prod_{t=T}^{T} \exp\left (-y_i\alpha_th_t({\bf x})\right) \\& =Z_1Z_2\cdots Z_{T}\sum_{i=1}^N D_{T + 1,i} \\& =Z_1Z_2\cdots Z_{T}\sum_{i=1}^N D_{T + 1,i} \hspace{7ex} \sum_{i=1}^N D_{T + 1,i}=1 \\& =\prod_{t=1}^TZ_t \end{align*} \] 即我们最小化\(\prod_{t=1}^TZ_t\)等价于最小化指数损失函数，我们可以在每一轮都最小化\(Z_t\) \[ \begin{align*} Z_t &= {\sum_{i=1}^N D_{t,i}}\cdot \exp\left(-y_i\alpha_th_t({\bf x_i}) \right) \\&= {\sum_{i: \ y_i \ne h_t(x_i)} D_{t,i}}\exp(\alpha_t) + {\sum_{i: \ y_i = h_t(x_i)} D_{t,i}}\exp(-\alpha_t) \\&= \epsilon_te^{\alpha_t} + (1 - \epsilon_t)e^{-\alpha_t} \end{align*}\tag{2-3} \] 对\(\alpha_t\)求导得得到权重公式： \[ \frac{\partial Z_t}{\partial \alpha_t} = \epsilon_te^{\alpha_t} - (1 - \epsilon_t)e^{-\alpha_t} = 0 \hspace{4ex}\Rightarrow \alpha_t= \frac{1}{2}\ln\frac{1-\epsilon_t}{\epsilon_t}\tag{2-4} \] 将2-4带入2-3得： \[ Z_t = 2\sqrt{\epsilon_t(1-\epsilon_t)} = \sqrt{1 - (1-2\epsilon_t)^2} = \sqrt{1 - 4\gamma_t^2} \hspace{4ex} 设\gamma_t = \frac{1}{2} - \epsilon_t \] 因此，2-1的训练误差界可以写为： \[ \frac{1}{N}\sum_{i=1}^N I \left(H({\bf x_i}) \ne y_i \right) \le \prod_{t}Z_t = \prod_{t} \sqrt{1 - 4\gamma_t^2} \le exp(-2\sum_{t=1}^T\gamma_t^2)\tag{2-5} \] 李航老师的书中说：2-5的最后一个式子可先由\(e^x\)和\(\sqrt{1-x}\)在点x = 0的泰勒展开式推出不等式\(\sqrt{1 - 4\gamma_t^2} \le exp(-2\gamma_t^2)\)进而得到。

这表明Adaboost的训练误差是以指数速率下降的。

PS： Adaboost能适应弱分类器各自的训练误差，这也是它的名字（适应的提升）的由来。Ada是Adaptive的简写。

加法模型和前向分布算法

本小节主要介绍加法模型。

Adaboost可以看出是加法模型、损失函数为指数损失函数、学习算法为前向分布算法时的二分类学习方法。此外，之后要介绍的GBDT也可以看出是加法模型。

加法模型即： \[ F({\bf x}) =\sum_{t=1}^T \alpha_t h_t({\bf x}; {\bf w_t}) = \sum_{i=1}^Tf_t({\bf x}; {\bf w_t}) \tag{3-1} \] 其中,\(h_t({\bf x}; {\bf w_t})\)为基学习器， \(\bf x\)为输入样本，\(\bf w\)为基学习器的参数，而\(\alpha_t\)为每个基学习器\(h_t\)的权重

可以通过最小化损失函数进行求解，即求经验风险极小化问题： \[ \min_{\alpha,\bf w} \sum_{i=1}^N L\left(y_i, \sum_{t=1}^T \alpha_t h_t({\bf x}; {\bf w_t})\right)\tag{3-2} \] 要求解这个问题，是NP难的，一般用贪心法进行求解，即前向分布算法：从前往后，每一步只学习一个基函数及其系数，逐步优化3-2式。前向分布算法可以描述如下：

输入: 训练集 \(Data =\{({\bf x_1},y_1),({\bf x_2},y_2),\cdots,({\bf x_N},y_N)\}, y_i \in\{+1, -1\}\);

​ 损失函数L

过程：

​ for t = 1 to T do

​ \((\alpha_t, w_t) = \arg\min_{\alpha_t,w_t} \sum_{i=1}^N L\left(y_i, f_{t-1}({\bf x_i}) + \alpha_t h_t({\bf x}; {\bf w_t})\right)\) # 得到参数和基学习器权重

​ 更新\(f_t({\bf x}) = f_{t-1}({\bf x_i}) + \alpha_t h_t({\bf x}; {\bf w_t})\)

得到加法模型

​ \(F({\bf x}) = f_{t}({\bf x}) = \sum_{t=1}^T \alpha_t h_t({\bf x}; {\bf w_t})\)

这样，便将同时求解t = 1到T的所有参数\(\alpha_t, \bf w_t\)的优化问题转化为逐步求解各个\(\alpha_t, \bf w_t\)的问题。

再谈Adaboost

上面说到，Adaboost是加法模型，损失函数为指数损失函数，并采用前向分布算法。

下面进行证明：

前向分布分布算法学习的是加法模型，当基函数为基本分类器时，该加法模型等价于Adaboost的最终分类器。\(H({\bf x}) = \sum_{t=1}^T \alpha_t h_t({\bf x})\)

指数损失函数

首先证明前向分布算法的损失函数是指数损失函数\(L(y, F({\bf x})) = \exp(-yF({\bf x}))\)时，其学习的具体操作等价于Adaboost算法学习的具体操作。

假设经过t - 1轮迭代前向分步算法已经得到\(f_{t-1}({\bf x}) = f_{t-2}({\bf x}) + \alpha_{t-1}h_{t-1}({\bf x}) = \alpha_{1}h_1({\bf x}) + \cdots + \alpha_{t-1}h_{t-1}({\bf x})\)

则在第t轮迭代应该寻找最优的\(\alpha_t, h_t\)使得指数损失最小即 \((\alpha_t, h_t) = \arg\min_{\alpha_t,h_t} \sum_{i=1}^N L\left(y_i, f_{t-1}({\bf x_i}) + \alpha_t h_t({\bf x})\right)\)

从而得到\(f_{t}({\bf x}) = f_{t-1}({\bf x}) + \alpha_{t}h_t({\bf x})\)。而指数损失最小可以写为： \[ \begin{align*} (\alpha_t, h_t) &=\mathop{\arg\min}_{\alpha_t,h_t} \sum_{i=1}^N \exp\left(-y_i(f_{t-1}({\bf x_i}) + \alpha_th_t({\bf x}))\right) \\ &=\mathop{\arg\min}_{\alpha_t,h_t} \sum_{i=1}^N D_{t,i}\exp\left( -y_i\alpha_th_t({\bf x})\right)\tag{3-3} \end{align*} \] 其中\(D_{ti} = Error_{(t-1,i)} = \exp(-y_if_{t-1}({\bf x_i}))\)与当前的优化目标无关，只与之前的有关，因此为指数损失函数。

基分类器求解和权重推导

接着证明使得式子3-3达到最小的\(\alpha_t^*\)和\(h_t^*({\bf x})\)就是Adaboost算法得到的\(\alpha_t\)和\(h_t({\bf x})\)。

求解3-3可以分为两步，首先求\(h_t({\bf x})\)，对于任意的\(\alpha_t \gt 0\)，使3-3最小的\(h_t({\bf x})\)由下式得到： \[ h_t^*({\bf x}) = \mathop{\arg\min}_h \sum_{i=1}^ND_{t,i}I(y_i\ne h({\bf x})) \] 其中\(D_{t,i}= \exp(-y_if_{t-1}(\bf x_i))\)。

这样就得到了基分类器\(h_t^*({\bf x})\)，而该分类器就是Adaboost算法的基本分类器\(h_t({\bf x})\)，因为它是第t轮加权训练数据分类误差率最小的基本分类器。

接下来求\(\alpha_t\), 式在3-3中： \[ \begin{align*} \sum_{i=1}^N D_{t,i}\exp\left( -y_i\alpha_th_t({\bf x})\right) & = \sum_{y_i=h_t(\bf x)}D_{t,i} e^{-\alpha} + \sum_{y_i\ne h_t(\bf x)}D_{t,i}e^{\alpha} \\ &=e^{-\alpha}\sum_{i=1}^ND_{t,i} + (e^{\alpha} - e^{-\alpha})\sum_{i=1}^N D_{t,i}I(y_i\ne h_t({\bf x_i})) \tag{3-4} \end{align*} \] 最后一个变换可以认为是第一项多加了不相等时候的\(e^{-\alpha}\), 因此在第二项的时候减去。1-8对\(\alpha\)求导，并使导数为0，得到使得3-3最小的\(\alpha_t\) \[ \alpha_t = \frac{1}{2} \ln(\frac{1 - \epsilon_t }{\epsilon_t}) \] 其中\(\epsilon_t\)为分类误差率 \[ \epsilon_t = \frac{\sum_{i=1}^N D_{t,i}I(y_i\ne h_t({\bf x}))}{\sum_{i=1}^N D_{t,i}} = \sum_{i=1}^N \tilde D_{t,i}I(h_t(x_i) \ne y_i) \] 可以看出和之前更新\(\alpha_t\)一致。

最后来看每一轮样本的权值更新，由\(f_{t}({\bf x}) = f_{t-1}({\bf x}) + \alpha_{t}h_t({\bf x})\)和\(D_{t,i}= \exp(-y_if_{t-1}(\bf x_i))\)可得： \[ \begin{align*} D_{t + 1,i} &= \exp(-y_if_{t}(\bf x_i))\\ &= \exp(-y_i( f_{t-1}({\bf x_i}) + \alpha_{t}h_t({\bf x_i}))\\ &= D_{(t,i)}\exp(- \alpha_{t}y_{i}h_t({\bf x_i}))\\ \end{align*} \] 这与之前的Adaboost的样本权值更新公式相比，只差规范化因子，因而等价。

GBDT

GBDT全称为：Gradient Boosting Decision Tree，即梯度提升决策树。可以理解为梯度 + 提升 + 决策树。

在介绍GBDT之前，先介绍比较简单的提升树（Boosting Decision Tree）

提升树

提升树实际上就是加法模型和前向分布算法，然后以CART决策树为基学习器。

可以表示为决策树的前向分布算法 \[ \begin{align*} F_0({\bf x}) &= 0\\ F_t({\bf x}) &= F_{t-1}({\bf x}) + h_t({\bf x}), t=1,2,\cdots ,T\\ F_T({\bf x}) &= \sum_{t=1}^Th_t({\bf x}) \end{align*} \]

在前向分布算法的第t步，给定当前模型\(F_{t-1}({\bf x})\)，需要求解 \[ h_t^*({\bf x}) = \mathop{\arg\min}_{h_t} \sum_{i=1}^NL(y_i, F_{t-1}({\bf x}) + h_t({\bf x})) \] 得到第t棵树\(F_{t}({\bf x})\)。针对不同问题的提升树学习方法，主要区别在于使用的损失函数不同。比如平方误差损失函数的回归问题，用指数损失函数的分类问题，以及用一般损失函数的问题。

采用平方损失函数时，有： \[ \begin{align*} L\left(y, F_{t-1}({\bf x}\right) + h_t({\bf x})) &=\left(y - F_{t-1}({\bf x} ) - h_t({\bf x})\right)^2\\ &=(r - h_t({\bf x}))^2 \end{align*} \] 其中\(r = y - F_{t-1}({\bf x})\) 称为残差(Residual)。因此，对回归树的提升树算法来说，只需要简单的拟合当前模型的残差即可。注意这里的是回归树。

因此回归问题的提升树算法可以描述如下：

输入: 训练集 \(Data =\{({\bf x_1},y_1),({\bf x_2},y_2),\cdots,({\bf x_N},y_N)\}, y_i \in\{+1, -1\}\);

过程：

​ 初始化\(F_0({\bf x}) = 0\)

​ for t = 1 to T do

​ 计算残差 \(r_{ti} = y_i - F_{t-1}({\bf x}) , \ i=1,2,\cdots,N\)

​ 拟合残差得到一个回归树：\(h_t({\bf x})\)

​ 更新\(F_t({\bf x}) = F_{t-1}({\bf x_i}) + h_t({\bf x})\)

得到加法模型\(F({\bf x}) = \sum_{t=1}^T h_t({\bf x})\)

该算法可以用下面的图表示：

Boosting tree

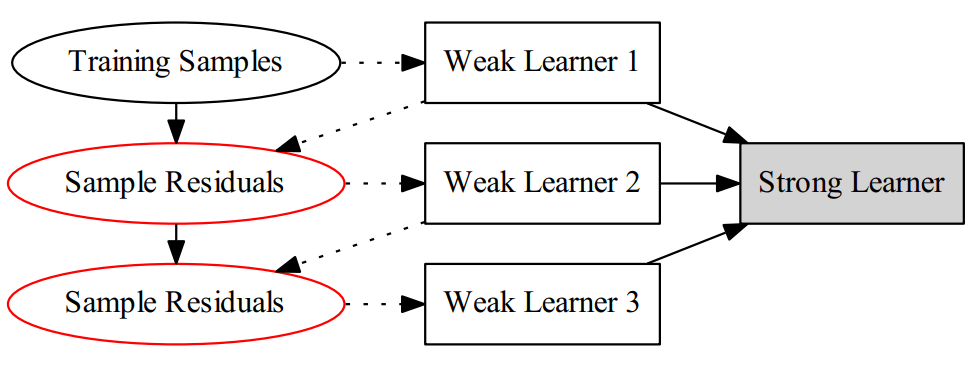
对比Adaboost来说，该算法可以说是修改样本的"label"，而AdaBoost则是修改样本的权重。

例子

继续搬出之前的决策树中的例子

x	1	2	3	4	5	6	7	8	9	10
y	5.56	5.70	5.91	6.40	6.80	7.05	8.90	8.70	9.00	9.05

第一轮计算后，我们算出（计算过程看决策树那章） \[ h_1(x) = \begin{cases} 6.24, & x\le 6.5 \\ 8.91, & x \gt 6.5 \\ \end{cases} \] 可以算出残差（比如x=1就是5.56 - 6.24 = -0.68）

x	1	2	3	4	5	6	7	8	9	10
y	-0.68	-0.54	-0.33	0.16	0.56	0.81	-0.01	-0.21	0.09	0.14

接着，继续拟合数据，只是拟合的是上面的残差。得到： \[ h_2(x) = \begin{cases} -0.52, & x\le 3.5 \\ 0.22, & x \gt 3.5 \\ \end{cases} \] 则\(f_2({\bf x})\)为： \[ F_2({\bf x}) = f_1({\bf x}) + f_2({\bf x}) = \begin{cases} 5.72, & x\le 3.5 \\ 6.46, & 3.5\lt x \le 6.5 \\ 9.13, & 6.5\lt x \end{cases} \] 以此类推进行计算即可，直到损失\(L(y, F_t(\bf x))\)满足要求，比如达到迭代次数T。

和决策树CART不同的地方在于，BDT每次拟合的是残差，而CART是经典的分治算法（divide and conquer），不断的划分子空间并在子空间中进一步精确的拟合。

梯度提升

前面提到过，GBDT全称为Gradient Boosting Decision Tree，梯度提升决策树。

现在我们来介绍通用的“梯度提升”算法。

当采用平方损失和指数损失的时候，每一步优化是很简单的，但是一般的损失函数来说，每一步的优化不容易，因此提出了梯度提升的方法，这是利用梯度下降的近似方法，其关键是利用损失函数的负梯度在当前模型的值： \[ -\left[\frac{\partial L(y_i, F({\bf x_i}))}{\partial F({\bf x_i})} \right]_{F({\bf x}) = F_{t-1}({\bf x})}\tag{4-1} \] 怎么理解这个近似呢？

以前面的均方损失函数为例，也是可以用这个方法来解释的。为了求导方便，我们在均方损失函数前乘以 1/2。 \[ \begin{align*} L(y_i, F({\bf x_i})) = \frac{1}{2}(y_i - F({\bf x_i}))^2 \end{align*} \] 注意到\(F({\bf x_i})\)其实只是一些数字而已，我们可以将其像变量一样进行求导： \[ \begin{align*} \frac{\partial L(y_i, F({\bf x_i}))}{\partial F({\bf x_i})} = F({\bf x_i}) - y_i \end{align*} \] 而前面所说的残差就是上式相反数，即负梯度： \[ r_{ti} = y_i - F_{t-1}({\bf x}) =-\left[\frac{\partial L(y_i, F({\bf x_i}))}{\partial F({\bf x_i})} \right]_{F({\bf x}) = F_{t-1}({\bf x})} \] 在梯度提升中，就是将式2-1作为残差来进行拟合。由此，我们给出一般的梯度提升算法：

输入: 训练集 \(Data =\{({\bf x_1},y_1),({\bf x_2},y_2),\cdots,({\bf x_N},y_N)\}, y_i \in\{+1, -1\}\);

过程：

​ 初始化\(F_0({\bf x}) =\mathop{\arg\min}_{h_0} \sum_{i=1}^NL(y_i, h_0({\bf x}))\)

​ for t = 1 to T do

​ 计算负梯度 \({\tilde y}_{i} = -\left[\frac{\partial L(y_i, F({\bf x_i}))}{\partial F({\bf x_i})} \right]_{F({\bf x}) = F_{t-1}({\bf x})} , \ i=1,2,\cdots,N\)

​ \(w_t = \arg\min_{w_t} \sum_{i=1}^N \left({\tilde y}_{i} - h_t({\bf x}; {\bf w_t})\right)^2\) # 拟合“残差“得到基学习器权重，也就得到了基学习器

​ \(\alpha_t= \arg\min_{\alpha_t} \sum_{i=1}^N L\left(y_i, f_{t-1}({\bf x_i}) + \alpha_t h_t({\bf x}; {\bf w_t})\right)\) # 得到基学习器权重\(\alpha_t\)

​ 更新\(F_t({\bf x}) = F_{t-1}({\bf x_i}) + \alpha_th_t({\bf x}; {\bf w_t})\)

对比提升树来说，提升树没有基学习器参权重\(\alpha_t\)

GBDT

至此，我们可以给出GBDT的算法了。就是采用梯度提升的决策树（CART）而已嘛。PS: 上面给出的是梯度提升。

前面提到过，CART回归将空间划分为K个不相交的区域。可以用数学公式描述为： \[ f(\mathbf{X}) = \sum_{k=1}^K c_k I(\mathbf{X} \in R_k) \] GBDT算法(回归)描述如下：

输入: 训练集 \(Data =\{({\bf x_1},y_1),({\bf x_2},y_2),\cdots,({\bf x_N},y_N)\}, y_i \in\{+1, -1\}\);

过程：

​ 初始化\(F_0({\bf x}) =\mathop{\arg\min}_{h_0} \sum_{i=1}^NL(y_i, h_0({\bf x})) =\mathop{\arg\min}_{c} \sum_{i=1}^NL(y_i, c))\)

​ for t = 1 to T do

​ 计算残差 \({\tilde y}_{i} = -\left[\frac{\partial L(y_i, F({\bf x_i}))}{\partial F({\bf x_i})} \right]_{F({\bf x}) = F_{t-1}({\bf x})} , \ i=1,2,\cdots,N\)

​ 拟合残差\({\tilde y}_{i}\)得到一个回归树，得到第t棵树的叶结点区域\(R_{tk}\)：\(h_t({\bf x})= \sum_{k=1}^K c_k I(\mathbf{X} \in R_{tk})\)

​ 更新\(F_t({\bf x}) = F_{t-1}({\bf x_i}) + h_t({\bf x}) = F_{t-1}({\bf x_i}) + \sum_{k=1}^K c_k I(\mathbf{X} \in R_{tk})\)

得到加法模型

​ \(F({\bf x}) = \sum_{t=1}^T h_t({\bf x})\)

可以说，如果我们的任务是回归的话，并且使用RMSE作为损失函数，就和上面的boosting tree一样。因为负梯度算出来就是残差:\(\left(y - F_{t-1}({\bf x} ) - h_t({\bf x})\right)^2=(r - h_t({\bf x}))^2\)

GBDT 分类

如果要将GBDT用于分类问题，怎么做呢？ 首先要明确的是，GBDT用于分类时使用的仍然是CART回归树。回想我们做回归问题的时候，每次对残差（负梯度）进行拟合。而分类问题要怎么每次对残差拟合？要知道类别相减是没有意义的。因此，可以用Softmax进行概率的映射，然后拟合概率的残差！

具体的做法如下：

1. 针对每个类别都先训练一个回归树，如三个类别，训练三棵树。就是比如对于样本\(\bf x_i\)为第二类，则输入三棵树分别为：\(({\bf x_i}, 0), ({\bf x_i},1); ({\bf x_i}, 0)\)这其实是典型的OneVsRest的多分类训练方式。 而每棵树的训练过程就是CART的训练过程。这样，对于样本\(\bf x_i\)就得出了三棵树的预测值\(F_1({\bf x_i}),F_2({\bf x_i}),F_3({\bf x_i})\)，模仿多分类的逻辑回归，用Softmax来产生概率，以类别1为例：\(p_{1}({\bf x_i})=\exp(F_{1}{({\bf x_i})})/\sum_{l= 1}^{3}\exp(F_{l}{({\bf x_i})})\)
2. 对每个类别分别计算残差，如类别1：\({\tilde y}_{i1}= 0 - p_1({\bf x_i})\), 类别2： \({\tilde y}_{i2}= 1 - p_2({\bf x_i})\)， 类别3：\({\tilde y}_{i3}= 0 - p_3({\bf x_i})\)
3. 开始第二轮的训练，针对第一类 输入为\(({\bf x_i}, {\tilde y}_{i1})\), 针对第二类输入为\(({\bf x_i}, {\tilde y}_{i2})\) ，针对第三类输入为 \(({\bf x_i}, {\tilde y}_{i3})\)，继续训练出三颗树。
4. 重复3直到迭代M轮，就得到了最后的模型。预测的时候只要找出概率最高的即为对应的类别。

和上面的回归问题是大同小异的。

被忽略的第三步

在原始的论文中，多分类的GBDT描述如下图（注意这里的m代表的是树的个数，N为样本数, K为类别数）

GBDT-classification

可以看出，和上面的一样，首先计算各个类的概率。然后对于每个类，计算出残差，然后用CART回归树拟合。这里和上面描述的是一样的。但是之后的倒数第五行那是什么鬼？在原论文中，描述为：拟合完后，每棵树有J个叶结点，对应区域\(\{R_{jkm}\}_{j=1}^J\)，模型通过下式的解更新这些\({\gamma}_{jkm}\) \[ {\gamma}_{jkm} = \mathop{\arg\min}_{\gamma_{jk}} \sum_{i=1}^N\sum_{k=1}^{K} \phi \left(y_{ik}, F_{k,m-1}({\bf x}) + \sum_{j=1}^J\gamma_{jk}I({\bf x_i} \in R_{jm})\right) \\ \phi(y_{k}, F_k)= -y_k\log p_k = p_{1}({\bf x_i})= -y_k\frac{exp(F_{k}{({\bf x_i})})}{\sum_{l= 1}^{K}exp(F_{l}{({\bf x_i})})} \] 但是这个式子没有闭式解。因此用牛顿法(Newton-Raphson step)进行近似。就是上面倒数第五行的结果。不过比较丢脸的是，这个我没有推出来。Sklearn中的GBDT实现中(MultinomialDeviance)，又略有不同，因此如果读者你会推的话就告诉博主把~

虽然说没有推出来，但是大多数情况下，可以通过设置步长（Step-size，也有的叫收缩率Shrinkage）的方式来省略这一步。因此很多资料很往往不介绍这一步。关于步长，本文最后有介绍。

Sklearn GBDT二分类实现 - BinomialDeviance

在GBDT二分类中，可以用Logistic函数进行概率映射，而可以不用多分类的SoftMax。

为了挽回一点面子，讲讲sklearn二分类的BinomialDeviance的实现。代码如下：

class BinomialDeviance(ClassificationLossFunction):
    ...
    def __call__(self, y, pred, sample_weight=None):
        """Compute the deviance (= 2 * negative log-likelihood). """
        # logaddexp(0, v) == log(1.0 + exp(v))
        pred = pred.ravel()
        if sample_weight is None:
            return -2.0 * np.mean((y * pred) - np.logaddexp(0.0, pred))
        else:
            return (-2.0 / sample_weight.sum() *
                    np.sum(sample_weight * ((y * pred) - np.logaddexp(0.0, pred))))

    def negative_gradient(self, y, pred, **kargs):
        """Compute the residual (= negative gradient). """
        return y - expit(pred.ravel())

首先是损失函数，忽略sample_weight权重设置，看看代码第八行。翻译过来就是 \[ -2.0 \frac{1}{N}(yP - \log(1 + exp(P))) \] 怎么感觉和对率损失不太一样？ \[ \begin{align*} L = -(y \log(h) + (1-y) \log(1 - h) &= -\left( \log(1 - h) + y \log \left( \frac{h}{1-h}\right) \right) \\ &=-\log(h(-P))- y P\hspace{4ex} 其中h(P) = \frac{1}{1+e^{-P}} \\ &=\log(1+ \exp(P)) - yP \end{align*} \] 这正是Sklearn使用的损失函数。

而负的梯度呢？ \[ -\frac{\partial L}{\partial P} = y - \frac{\exp(P)}{1+ \exp(P)} = y- h(P) \] 就是上面的y - expit(pred.ravel())

再来看看牛顿法更新：

def _update_terminal_region(self, tree, terminal_regions, leaf, X, y,
                            residual, pred, sample_weight):
    terminal_region = np.where(terminal_regions == leaf)[0]
    residual = residual.take(terminal_region, axis=0)
    y = y.take(terminal_region, axis=0)
    sample_weight = sample_weight.take(terminal_region, axis=0)

    numerator = np.sum(sample_weight * residual)
    denominator = np.sum(sample_weight * (y - residual) * (1 - y + residual))

    # prevents overflow and division by zero
    if abs(denominator) < 1e-150:
        tree.value[leaf, 0, 0] = 0.0
        else:
            tree.value[leaf, 0, 0] = numerator / denominator

主要查看numerator和denominator的计算，这里\(residual = y - h(P)\)

分子就是上面的负梯度，即\(residual = y - h(P)\)

分母为二阶导，即\(h(P)(1-h(P))= (y-residual)*(1-y+residual))\)

GBDT 正则化

为了避免过拟合，可以从两方面入手：

• 弱算法的个数T， 上面描述的算法中，记得么？就是迭代T轮。T的大小就影响着算法的复杂度
• 步长（Shrinkage）在每一轮迭代中，原来采用\(F_t({\bf x}) = F_{t-1}({\bf x}) + \alpha_th_t({\bf x}; {\bf w_t})\)进行更新，可以加入步长v，使得一次不更新那么多：\(F_t({\bf x}) = F_{t-1}({\bf x}) + v \ \alpha_th_t({\bf x}; {\bf w_t}); v\in(0,1]\)

参考资料

• 机器学习技法 - 林轩田
• 《机器学习》 - 周志华
• 《统计学习方法》 - 李航

关于Adaboost还可以查阅：

• Boosting Can we make dumb learners smart
• Adaboost - 新的角度理解权值更新策略

关于GBDT可以查阅

• Greedy Function Approximation: A Gradient Boosting Machine
• A Gentle Introduction to Gradient Boosting
• https://www.cnblogs.com/ModifyRong/p/7744987.html