leetcode 动态规划（DP）

本次题解包括

53. Maximum Subarray
62. Unique Paths
63. Unique Paths II
64. Minimum Path Sum
70. Climbing Stairs
72. Edit Distance
87. Scramble String
91 . Decode Ways
97. Interleaving String
115 Distinct Subsequences
120. Triangle
139. Word Break
140. Word Break II
152. Maximum Product Subarray
174 . Dungeon Game
198. House Robber
213 . House Robber II
221 . Maximal Square
712. Minimum ASCII Delete Sum for Two Strings
718. Maximum Length of Repeated Subarray
799. Champagne Tower
818. Race Car

53. Maximum Subarray

Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [-2,1,-3,4,-1,2,1,-5,4], the contiguous subarray [4,-1,2,1] has the largest sum = 6.

More practice:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

题目地址：leetcode Maximum Subarray

题目大意：给定一串数字，要求求出连续的序列，使得这个连续序列的和最大

水水的DP~

当前和为sum,如果sum >0,那么加上当前元素，否则sum=A[i] （即抛弃负数的sum，重新开始。因为负数的sum是累赘- -好难听的样子）

C++

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int cur = 0, ans = nums[0];
        for(int i = 0; i < nums.size(); ++i){
            cur += nums[i];
            if(cur > ans)
                ans = cur;
            if(cur < 0)
                cur = 0;
        }
        return ans;
    }
};

Python

class Solution(object):
    def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        ans, cur = nums[0], 0
        for x in nums:
            cur += x
            if cur > ans:
                ans = cur
            if cur < 0:
                cur = 0
        return ans

分治法

《编程珠玑》里其实有讲过。最大值要么在左边要么在中间，还有就是中间的情况

左右两边可以递归没什么好说的。

中间的就是从mid到left找最大的left_sum，以及从mid+1到right找最大的right_sum，就是left_sum + right_sum

C++

class Solution {
	int divide_and_conquer(int l, int r, const vector<int> &nums) {
		if (l == r) return nums[l];
		int mid = (l + r) >> 1;
		int left = INT_MIN, right = left;
		int cur = 0;
		for (int i = mid; i >= l; --i) {
			cur += nums[i];
			if (cur > left)
				left = cur;
		}
		cur = 0;
		for (int i = mid + 1; i <= r; ++i) {
			cur += nums[i];
			if (cur > right)
				right = cur;
		}
		return max(left + right, max(divide_and_conquer(l,mid,nums), divide_and_conquer(mid + 1, r, nums)));
	}

public:
	int maxSubArray(vector<int>& nums) {
		return divide_and_conquer(0, nums.size() - 1, nums);
	}
};

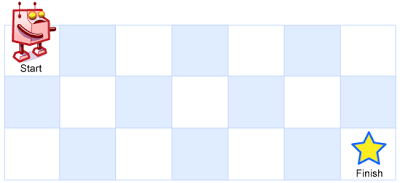
62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Above is a 3 x 7 grid. How many possible unique paths are there?

Note:_m_ and n will be at most 100.

题目地址：leetcode Unique Paths

题目大意: :从m*n大小的图中左上方走到右下方，每次只能向右或者向下，问一共有多少种走法

思路：

设dp[i][j]为到坐标为（i,j）的方法数，则有dp[i][j]= dp[i-1][j]+dp[i][j-1] 水~
这是看了discuss里面，有人用数学方法做的。 orz 原文如下:

It's true that this can be solved with dynamic programming. But you can see that every path has exactly m - 1 horizontal moves and n - 1 vertical moves. So, to get a particular path, you need to choose where to put your m - 1 horizontal moves (or your n - 1 vertical moves) amongst the m + n - 2 total moves. That gives (m+n-2 choose m-1) paths (or (m+n-2 choose n-1), which is the same).

C++

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for(int i = 0; i < n; ++i) dp[0][i] = 1;
        for(int i = 0; i < m; ++i) dp[i][0] = 1;
        
        for(int i = 1; i < m; ++i)
            for(int j = 1; j < n; ++j)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m - 1][n - 1];
    }
};

Python方法1

class Solution:
    # @return an integer
    def uniquePaths(self, m, n):
        dp =[[0 for i in range(n+1)]  for i in range(m+1)]
        for i in range(1,n+1):
            dp[1][i] = 1
        for i in range(2,m+1):
            for j in range(1,n+1):
                dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[m][n]

Python 方法2

class Solution:
    # @return an integer
    def uniquePaths(self, m, n):
        return math.factorial(m+n-2)/(math.factorial(n-1)*math.factorial(m-1))

63. Unique Paths II

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.
1
2
3
4
5
6
[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]
The total number of unique paths is 2.

Note:_m_ and n will be at most 100.

题目地址：leetcode Unique Paths II

题目大意: 和上面一题差不多，都是要求从左上角到右下角的方法数，只不过这题有障碍物，有障碍物的不能走。

思路：还是dp，就稍微改下即可。设dp[i][j]为到坐标为（i,j）的方法数。对于(i,j):

(i,j)为障碍物，则dp[i][j]=0
(i,j)不为障碍物则 dp[i][j]= dp[i-1][j]+dp[i][j-1]

C++

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid.empty()  obstacleGrid[0].empty()) return 0;
        
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[0][0] = obstacleGrid[0][0] ^ 1;
        
        for(int i = 1; i < n; ++i) dp[0][i] = dp[0][i - 1] & (!obstacleGrid[0][i]);
        for(int i = 1; i < m; ++i) dp[i][0] = dp[i - 1][0] & (!obstacleGrid[i][0]);
        
        for(int i = 1; i < m; ++i)
            for(int j = 1; j < n; ++j)
                dp[i][j] = obstacleGrid[i][j]? 0 : dp[i - 1][j] + dp[i][j - 1];
        return dp[m - 1][n - 1];
    }
};

Python

class Solution:
    # @param obstacleGrid, a list of lists of integers
    # @return an integer
    def uniquePathsWithObstacles(self, obstacleGrid):
        m , n = len(obstacleGrid) , len(obstacleGrid[0])
        dp = [[0 for x in range(n+1)] for x in range(m+1)]
        for j in range(1,n+1):
            if obstacleGrid[0][j-1]:
                break
            else:
                dp[1][j] = 1
                
        for i in range(2,m+1):
            for j in range(1,n+1):
                if obstacleGrid[i-1][j-1]:
                    dp[i][j] = 0
                else:
                    dp[i][j]=dp[i-1][j]+dp[i][j-1]
        return dp[m][n]

64. Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

题目地址：leetcode Minimum Path Sum

题目大意: mn的格子中有mn个非负整数，求从左上角到右下角中，经过的数字和的最小值（每次只能向右或者向下走）

思路:水题，其实和上面的也差不多。继续dp。

设dp[i][j]为当前到达坐标为(i,j)的最小和，dp[i][j]=min(dp[i - 1][j], dp[i][j - 1]) + grid[i ][j ];

我的版本由于dp数组和grid坐标差了1所以为min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];

其实也可以O(N)的空间实现的。

C++

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if(grid.empty()  grid[0].empty()) return 0;
        
        int m = grid.size(), n = grid[0].size(); 
        vector<vector<int>> dp(m, vector<int>(n, 0));
        
        dp[0][0] = grid[0][0];
        for(int i = 1; i < n; ++i) dp[0][i] = dp[0][i - 1] + grid[0][i];
        for(int i = 1; i < m; ++i) dp[i][0] = dp[i - 1][0] + grid[i][0];
        
        for(int i = 1; i < m; ++i)
            for(int j = 1; j < n; ++j)
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        
        return dp[m - 1][n - 1];
    }
};

版本2

class Solution {
public:	
	int minPathSum(vector<vector<int>> &grid) {
		int m = grid.size(), n = grid[0].size();
		vector<vector<int>> dp(m+1, vector<int>(n+1, 0x7ffffff));
		dp[0][1] = dp[1][0] = 0;
		for (int i = 1; i <= m; i++)
			for (int j = 1; j <= n; j++)
			dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];				
		return dp[m][n];
	}
};

Python

class Solution:
    # @param grid, a list of lists of integers
    # @return an integer
    def minPathSum(self, grid):
        m , n = len(grid) , len(grid[0])
        dp = [[0x7fffffff for x in range(n+1)] for x in range(m+1)]
        dp[0][1] = dp[1][0] = 0             
        for i in range(1,m+1):
            for j in range(1,n+1):
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1]
        return dp[m][n]

70. Climbing Stairs

You are climbing a stair case. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top? Note: Given n will be a positive integer.

题目地址：leetcode Climbing Stairs

题目大意: 爬楼梯，每次可以爬一步或者两步，求从1爬到n的方法数

思路：水~ dp[i] = dp[i - 1] + dp[i - 2];

class Solution {
public:
    int climbStairs(int n) {
        vector<int> f(n + 1, 0);
        f[1] = 1;
        f[2] = 2;
        f[3] = 3;
        if(n <= 3) return f[n];
        for(int i = 4; i <= n; ++i)
            f[i] = f[i - 1] + f[i - 2];
        return f[n];
    }
};

但只需三个变量即可。

C++

class Solution {
public:
	int climbStairs(int n) {
		int zero = 0, one = 1, two=1;
		for (int i = 1; i <= n; i++){
			two = zero + one;
			zero = one;
			one = two;
		}
		return two;
	}
};

Python

class Solution(object):
    def climbStairs(self, n):
        """
        :type n: int
        :rtype: int
        """
        zero, one, two = 0, 1, 1
        for i in range(1, n + 1):
            two = zero + one
            zero, one = one, two
        return two

还可以用矩阵快速幂的方法:

设Q^n如下： \[Q^n = \left[ \begin{matrix} f_{n+1} & f_{n} \\ f_{n} & f_{n-1} \\ \end{matrix} \right] \\ 初始值Q^1= \left[ \begin{matrix} 1 &1 \\ 1 & 0 \\ \end{matrix} \right] \\\]

可以用数学归纳法证明：

\[\begin{alignat}{2}Q^k &= \left[ \begin{matrix} f_{k+1} & f_{k} \\ f_{k} & f_{k-1} \\ \end{matrix} \right] \end{alignat}\]

\[\begin{alignat}{2}Q^{k+1} &= \left[ \begin{matrix} f_{k+1} & f_{k} \\ f_{k} & f_{k-1} \\ \end{matrix} \right] \left[ \begin{matrix} 1 &1 \\ 1 & 0 \\ \end{matrix} \right] \\& = \left[ \begin{matrix} f_{k+1}+f_{k} &f_{k+1} \\ f_{k+1} & f_{k} \\ \end{matrix} \right] \\& = \left[ \begin{matrix} f_{k+2} &f_{k+1} \\ f_{k+1} & f_{k} \\ \end{matrix} \right] \end{alignat}\]

C++ 复杂度O(Logn)

class Solution {
public:
    int climbStairs(int n) {
        vector<vector<int>> f = {{1, 1}, {1, 0}};
        vector<vector<int>> ans(f);
        while(n){
            if(n & 1)
                ans = mul(ans, f);
            f = mul(f, f);
            n >>= 1;
        }
        return ans[0][1];
    }
    
    vector<vector<int>> mul(const vector<vector<int>> &a, const vector<vector<int>> &b){
       vector<vector<int>> res(a.size(), vector<int>(b[0].size(), 0));
        for(int i = 0; i < a.size(); ++i)
            for(int j = 0; j < a[0].size(); ++j)
                for(int k = 0; k < b.size(); ++k)
                    res[i][j] += a[i][k] * b[k][j];
        return res;
    }
};

72. Edit Distance

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

Insert a character

Delete a character

Replace a character

题目地址：leetcode Edit Distance

题目大意：给定两个字符串，求他们的编辑距离（即可以插入、修改、删除一个字符，用最少的步数使得一个字符串变为另一个字符串）

思路:设dp[i][j]为以i和j结尾的字符串的编辑距离。

if word[i] == word[j] ： dp[i][j] = dp[i-1][j-1]
if word[i] != word[j] ： dp[i][j] 下面三个数的最小值+1：
- dp[i-1][j] 可以看为word1[i-1]然后插入一个字符（word2[j]),或者说删掉 word2[j]
- dp[i][j-1] 可以看为word2[j-1]然后插入一个数(word1[i])，或者说删掉 word1[i]
- dp[i-1][j-1]把word1[i]改为word2[j]，或者word2[j]改为word1[i]

还可以只用O(n)空间, 见java版本。其他语言其实类似，不想写了。

C++

class Solution {
 public:
	 int minDistance(string word1, string word2) {
		 int m = word1.size(), n = word2.size();
		 vector<vector<int> > dp(m+1, vector<int>(n+1, 0));
		 for (int i = 1; i <= m; i++) dp[i][0] = i;
		 for (int j = 1; j <= n; j++) dp[0][j] = j;
		 for (int i = 1; i <= m; i++)
		 {
			 for (int j = 1; j <= n; j++)
			 {
				 if (word1[i - 1] == word2[j - 1])
					 dp[i][j] = dp[i - 1][j - 1];
				 else
					 dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
			 }
		 }
		 return dp[m][n];
	 }
 };

Python

class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        dp = [[0] * (len(word2) + 1) for _ in range(len(word1) + 1)]
        for i in range(len(word1) + 1): dp[i][0] = i
        for j in range(len(word2) + 1): dp[0][j] = j

        for i in range(1, len(word1) + 1):
            for j in range(1, len(word2) + 1):
                if word1[i - 1] == word2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
        return dp[-1][-1]

Java

因为只用到左上方，左边，和上边的元素，所以可以只用两个数组。

class Solution {
    public int minDistance(String word1, String word2) {
        int[] dp = new int[word2.length() + 1];
        for (int j = 0; j <= word2.length(); j++) dp[j] = j;

        for (int i = 1; i <= word1.length(); i++) {
            int[] ndp = new int[word2.length() + 1];
            ndp[0] = i;
            for (int j = 1; j <= word2.length(); j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1))
                    ndp[j] = dp[j - 1];
                else
                    ndp[j] = Math.min(ndp[j - 1], Math.min(dp[j - 1], dp[j])) + 1;
            }
            dp = ndp;
        }
        return dp[word2.length()];
    }
}

87. Scramble String

Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively.

Below is one possible representation of s1 = "great":
1
2
3
4
5
6
7
8
    great
   /    \
  gr    eat
 / \    /  \
g   r  e   at
           / \
          a   t
To scramble the string, we may choose any non-leaf node and swap its two children.

For example, if we choose the node "gr" and swap its two children, it produces a scrambled string "rgeat".
1
2
3
4
5
6
7
8
    rgeat
   /    \
  rg    eat
 / \    /  \
r   g  e   at
           / \
          a   t
We say that "rgeat" is a scrambled string of "great".

Similarly, if we continue to swap the children of nodes "eat" and "at", it produces a scrambled string "rgtae".
1
2
3
4
5
6
7
8
    rgtae
   /    \
  rg    tae
 / \    /  \
r   g  ta  e
       / \
      t   a
We say that "rgtae" is a scrambled string of "great".

Given two strings s1 and s2 of the same length, determine if s2 is a scrambled string of s1.

题目地址：leetcode Scramble String

题目大意：给定两个字符串s1和s2，判断s2是否是s1经过旋转得到的。

思路：

根据题目的描述，我们可以枚举切分点i,然后递归判断:

s1[0, i-1]和s2[0, i-1] 是否可以旋转得到，并且s1[i, n - 1]和s2[i, n- 1] 也要能旋转得到
或者s1[0, i - 1]和s2[n - i, n - 1] 是否可以旋转得到，并且s1[i, n- 1]和s2[0, n - i] 也要能旋转得到

可以用记忆化搜索防止重复搜索，还可以用排序剪枝（看看当前的s1和s2排序后是否相等）

C++

class Solution {
    bool judge(string s1, string s2, unordered_map<string, bool> &vis){
        if(s1.size() != s2.size()) return false;
        if(s1 == s2) return true;
        if(vis.find(s1 + s2) != vis.end()) return vis[s1 + s2];
        
        string t1(s1), t2(s2);
        sort(t1.begin(), t1.end());
        sort(t2.begin(), t2.end());
        
        if(t1 == t2){
            for(int i = 1; i < s2.size(); ++i){
                if(judge(s1.substr(0, i), s2.substr(0, i), vis) &&
                  judge(s1.substr(i), s2.substr(i), vis))
                    return true;
                if(judge(s1.substr(0, i), s2.substr(s2.size() - i), vis) &&
                  judge(s1.substr(i), s2.substr(0, s2.size() - i), vis))
                    return true;
            }
        }
        return vis[s1 + s2] = false;
    }
    
public:
    bool isScramble(string s1, string s2) {
        unordered_map<string, bool> vis;
        return judge(s1, s2, vis);
    }
};

Python

class Solution(object):
    def judge(self, s1, s2, dp):
        if (s1, s2) in dp:
            return dp[s1, s2]
        if s1 == s2:
            dp[s1, s2] = True
            return True
        
        if sorted(s1) != sorted(s2):
            return False

        for i in range(1, len(s1)):
            if self.judge(s1[:i], s2[:i], dp) and self.judge(s1[i:], s2[i:], dp) or \
                    self.judge(s1[:i], s2[-i:], dp) and self.judge(s1[i:], s2[:-i], dp):
                dp[s1, s2] = True
                return True

        dp[s1, s2] = False
        return False

    def isScramble(self, s1, s2):
        """
        :type s1: str
        :type s2: str
        :rtype: bool
        """
        if len(s1) != len(s2): return False
        dp = {}
        return self.judge(s1, s2, dp)

91. Decode Ways

A message containing letters from A-Z is being encoded to numbers using the following mapping:

'A' -> 1 'B' -> 2 ... 'Z' -> 26

Given an encoded message containing digits, determine the total number of ways to decode it.

For example, Given encoded message "12", it could be decoded as "AB" (1 2) or "L" (12).

The number of ways decoding "12" is 2.

题目地址：leetcode Decode Ways

题目大意：给定一个数字组成的字符串，让你看有多少种解码方式

思路：

对于一个编码后的串s，s的所有的字符出现在0~9之间。

要查看其解码方式有多少种可能，主要在于因为有的字符可以被拆分，如12可以算L也可以算AB，而这样的在10~26均是可能的。

设dp[i]为s[0...i]最多的解码方式，因此我们有：

若s[i] !='0' , dp[i] += dp[i-1]
若10 <= s[i-1,i] <=26 , dp[i] += dp[i-2]

class Solution(object):
    def numDecodings(self, s):
        """
        :type s: str
        :rtype: int
        """
        if not s: return 0
        n = len(s)
        dp = [0] * n
        dp[0] = 1 if s[0] != '0' else 0
        for i in range(1, n):
            if 10 <= int(s[i - 1:i + 1]) <= 26:
                dp[i] += dp[i - 2] if i >= 2 else 1
            if s[i] != '0':
                dp[i] += dp[i - 1]
        return dp[n - 1]

C++

感觉第二次写的C++版本更清晰一些。

若s[i] !='0',
- dp[i] += dp[i-1]
- 若10 <= s[i-1,i] <=26 , dp[i] += dp[i-2]
s[i] =='0' ,
- 看看是否能和前面的合并。不能就返回0，可以就是dp[i-2]

class Solution {
public:
	int numDecodings(string s) {
		if (s[0] <= '0')
			return 0;
		vector<int> dp(s.size(), 0);
		dp[0] = 1;
		for (int i = 1; i < s.size(); ++i) {
			if (s[i] < '0' && s[i] > '9' || s[i] == '0' && s[i - 1] == '0')
				break;
			if (s[i] != '0')
				dp[i] = dp[i - 1];
			if (s[i - 1] == '1' || s[i - 1] == '2' && s[i] <= '6')
				dp[i] += i < 2 ? 1 : dp[i - 2];
		}
		return dp[s.size() - 1];
	}
};

97. Interleaving String

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.

For example, Given: s1 = "aabcc", s2 = "dbbca",

When s3 = "aadbbcbcac", return true. When s3 = "aadbbbaccc", return false.

题目地址：leetcode Interleaving String

题目大意：给定s1,s2,s3三个字符串，判断s3是否由s1和s2组成。

思路:设dp[i][j]为s1[i-1] , s2[j-1] 是否能组成 s3[i+j-1]

dp[i][j] = s3[i+j-1]==s1[i-1] && dp[i-1][j] s3[i+j-1]==s2[j-1] && dp[i][j-1]; (尝试用s1[i-1]去匹配，故应该是dp[i-1][j]，同理用s2[j-1]去匹配）

C++

class Solution {
public:
	bool isInterleave(string s1, string s2, string s3) {
		if (s1.size() + s2.size() != s3.size()) return false;
		vector<vector<bool>> dp(s1.size() + 1, vector<bool>(s2.size() + 1, false));

		dp[0][0] = true;
		for (int i = 1; i <= s1.size(); ++i)
			dp[i][0] = dp[i - 1][0] && s3[i - 1] == s1[i - 1];

		for (int j = 1; j <= s2.size(); ++j)
			dp[0][j] = dp[0][j - 1] && s3[j - 1] == s2[j - 1];

		for (int i = 1; i <= s1.size(); ++i)
			for (int j = 1; j <= s2.size(); ++j)
				dp[i][j] = (dp[i - 1][j] && s3[i + j - 1] == s1[i - 1]) || (dp[i][j - 1] && s3[i + j - 1] == s2[j - 1]);
		return dp[s1.size()][s2.size()];
	}
};

Python

class Solution(object):
    def isInterleave(self, s1, s2, s3):
        """
        :type s1: str
        :type s2: str
        :type s3: str
        :rtype: bool
        """
        m, n = len(s1), len(s2)
        if len(s3) != m + n: return False
        dp = [[False] * (n + 1) for _ in range(m + 1)]
        dp[0][0] = True
        for i in range(1, m + 1):
            dp[i][0] = dp[i - 1][0] and s1[i - 1] == s3[i - 1]
        for j in range(1, n + 1):
            dp[0][j] = dp[0][j - 1] and s2[j - 1] == s3[j - 1]

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                dp[i][j] = (dp[i - 1][j] and s1[i - 1] == s3[i + j - 1]) \
                           or (dp[i][j - 1] and s2[j - 1] == s3[i + j - 1])
        return dp[m][n]

115. Distinct Subsequences

Given a string S and a string T, count the number of distinct subsequences of T in S.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

Here is an example: S = "rabbbit", T = "rabbit"

Return 3.

题目地址：leetcode Distinct Subsequences

题目大意：给定S和T两个字符串，问把通过删除S中的某些字符，把S变为T有几种方法？

思路：DP,设dp[i][j]为到S[i] T[j]位置的方法数：

S[i]==T[j]: dp[i][j] = dp[i-1][j] + dp[i-1][j-1] 两字符串相等，要么跳过不匹配，要么匹配
S[i]!=T[j]: dp[i][j]= dp[i-1][j]不相等只能不匹配这个

初始值设置：

dp[i][0] = dp[i - 1][0] + (s[i] == t[0]) 即t[0]可以被s表示的数量

C++

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = s.size(), n = t.size();
        if(n > m) return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        
        for(int i = 0; i < m; ++i)
            dp[i][0] = (s[i] == t[0]) + (i > 0? dp[i - 1][0] : 0);
            
        for(int i = 1; i < m; ++i){
            for(int j = 1; j < n; ++j){
                if(s[i] == t[j])
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                else
                    dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[m - 1][n - 1];
    }
};

另一种写法：

C++

class Solution {
public:
	int numDistinct(string s, string t) {
		int m = s.size(), n = t.size();
		vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
		for (int i = 0; i <= m; i++) dp[i][0] = 1;
		for (int i = 1; i <= m; i++) {
			for (int j = 1; j <= n; j++) {
				if (s[i - 1] == t[j - 1])
					dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
				else
					dp[i][j] = dp[i - 1][j];
			}
		}
		return dp[m][n];

	}
};

Python

class Solution:
    # @return an integer
    def numDistinct(self, S, T):
        m , n = len(S),len(T)
        dp =[[0 for j in range(n+1)]for i in range(m+1)]
        for i in xrange(0,m+1): dp[i][0]=1
    
        for i in xrange(1,m+1):
            for j in xrange(1,n+1):
                if S[i-1]==T[j-1]:
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j]
                else:
                    dp[i][j]=dp[i-1][j]

        return dp[m][n]

120. Triangle

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle
1
2
3
4
5
6
[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

题目地址：leetcode Triangle

题目大意：给定一个三角形，求其从顶部到底部最小的和。

思路：DP，可以从上往下也可以从下往上

从下往上的版本:

C++

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()  triangle[0].empty()) return 0;
        vector<int> dp(triangle.back());
        for(int i = triangle.size() - 2; i >= 0; --i)
            for(int j = 0; j <= i; ++j)
                dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j];
        
        return dp[0];
    }
};

Python

class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        dp = triangle[-1]
        for i in range(len(triangle) - 2, -1, -1):
            next_dp = [0] * len(triangle[i])  
            for j in range(i + 1):
                next_dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]
            dp = next_dp
        return dp[0]

从下往上的版本：

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        if(triangle.empty()  triangle[0].empty()) return 0;
        vector<int> dp(triangle.size() + 1, INT_MAX);
        dp[0] = triangle[0][0];
        for(int i = 1; i < triangle.size(); ++i){
            vector<int> next(triangle.size() + 1, INT_MAX);
            for(int j = 0; j <= i; ++j)
                next[j] = min((j > 0? dp[j - 1]:INT_MAX), dp[j]) + triangle[i][j];
            dp = next;
        }
        return *min_element(dp.begin(), dp.end());
    }
};

139. Word Break

Given a string s and a dictionary of words dict, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

For example, given s = "leetcode", dict = ["leet", "code"].

Return true because "leetcode" can be segmented as "leet code".

传送门

题意：给定一个字符串s和字典，判断字符串s是否能拆成仅由字典组成的若干个单词？

思路：dp ，设dp[i]为 [0,i-1]是否能拆分

dp[i+1]= true dp[j] =true && s[j,i]在字典中）

class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: Set[str]
        :rtype: bool
        """
        n , dp = len(s),[True] + [False]*len(s)
        for i in xrange(n):
            for j in xrange(i+1):
                if dp[j] and s[j:i+1] in wordDict:
                    dp[i+1]=True
                    break
        return dp[n]

140. Word Break II

Given a string s and a dictionary of words dict, add spaces in s to construct a sentence where each word is a valid dictionary word.

Return all such possible sentences.

For example, given s = "catsanddog", dict = ["cat", "cats", "and", "sand", "dog"].

A solution is ["cats and dog", "cat sand dog"].

传送门

题意：给定一个字符串s和字典，将字符串s拆成仅由字典组成的若干个单词，返回所有的解

思路：在DFS的过程中，判断接下来的过程中是否有解。（就是进行剪枝操作啦），判断是否有解类似139那题。

Python

class Solution(object):
    def wordBreak(self, s, wordDict):
        """
        :type s: str
        :type wordDict: Set[str]
        :rtype: List[str]
        """
        ans = []
        if self.check(s, wordDict):
            self.dfs(0, len(s), '', s, ans, wordDict)
        return ans

    def check(self, s, wordDict):
        dp = [True] + [False] * len(s)
        n = len(s)
        for i in xrange(n):
            for j in xrange(i + 1):
                if dp[j] and s[j:i + 1] in wordDict:
                    dp[i + 1] = True
                    break
        return dp[n]

    def dfs(self, cur, n, path, s, ans, wordDict):
        if cur == n:
            ans.append(path)
            return

        for i in xrange(cur, n):
            if s[cur:i + 1] in wordDict and self.check(s[i + 1:n], wordDict):
                if path:
                    self.dfs(i + 1, n, path + ' ' + s[cur:i + 1], s, ans, wordDict)
                else:
                    self.dfs(i + 1, n, s[cur:i + 1], s, ans, wordDict)

152. Maximum Product Subarray

Find the contiguous subarray within an array (containing at least one number) which has the largest product.

For example, given the array [2,3,-2,4], the contiguous subarray [2,3] has the largest product = 6.

传送门

题意：给定一个数组，求连续的乘积最大值。

思路：dp，设f(k)为乘积最大序列，g(k)为成绩最小序列，则有

f(k) = max( A[k] , f(k-1) * A[k], A[k], g(k-1) * A[k] )
g(k) = min(A[k], g(k-1) * A[k], A[k], f(k-1) * A[k] )

之所以要维护一个最小的序列，是因为负数*负数变成正数，此时可能为最大。

class Solution:
    # @param A, a list of integers
    # @return an integer
    def maxProduct(self, A):
        maxMul = minMul = ans = A[0]
        for i in range(1, len(A)):
            t = maxMul
            maxMul = max(t * A[i], minMul * A[i], A[i])
            minMul = min(t * A[i], minMul * A[i], A[i])
            ans = max(maxMul, ans)
        return ans

174. Dungeon Game

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0's) or contain magic orbs that increase the knight's health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight's minimum initial health so that he is able to rescue the princess.

For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

-2 (K) -3 -3

5 -10 1

-10 30 -5 (P)

Notes:

The knight's health has no upper bound.

Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

-2 (K)	-3	-3
5	-10	1
-10	30	-5 (P)

题目地址：leetcode Dungeon Game

题目大意：一个骑士从左上角出发，要到达右下角拯救公主，每个格子中有正数表示可以增加的生命值，负数表示减少的生命。如果生命值为0，那么骑士就死翘翘了。你的任务是帮骑士计算到达右下角的最小生命值。

思路：DP，设dp[i][j]为到达(i,j)需要的最少生命值。则有：

dp[i][j]= max(1, min(dp[i+1][j],dp[i][j+1])-dungeon[i][j])

即从右下角到左上角进行计算:

对于dungeon为正数，减去说明生命值可以少一些到达这个格子（但是不能小于等于0）
对于负数，减去一个负数意味着加上这个数的绝对值，即需要的生命数增加

为什么是右下角到左上角而不是左上到右下呢？

如果途中遇到一个很大的正数，它就会覆盖掉你之前走过的所有信息。（变为0），这样的结果是错误的。

C++

class Solution {
public:
	int calculateMinimumHP(vector<vector<int>>& dungeon) {
		if (dungeon.empty())
			return 0;
		int m = dungeon.size(), n = dungeon[0].size();
		vector<vector<long long>> dp(m + 1, vector<long long>(n + 1, INT_MAX));
        dp[m - 1][n] = dp[m][n - 1] = 1;
		for (int i = m - 1; i >= 0; --i) {
			for (int j = n - 1; j >= 0; --j) {
				dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
                if(dp[i][j] <= 0)
                    dp[i][j] = 1;
			}
		}
		return dp[0][0];
	}
};

Python

class Solution(object):
    def calculateMinimumHP(self, dungeon):
        """
        :type dungeon: List[List[int]]
        :rtype: int
        """
        if not dungeon: return 0
        m, n = len(dungeon), len(dungeon[0])
        dp = [[0x7ffffff] * (n + 1) for _ in range(m + 1)]
        dp[m - 1][n] = dp[m][n - 1] = 1
        for i in range(m - 1, -1, -1):
            for j in range(n - 1, -1, -1):
                dp[i][j] = max(1, min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j])
        return dp[0][0]

198. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

传送门

题意：要求从一串数字中选取一些数，使得和最大（相邻不能两两）

思路：dp[i]为到i能获得的最大值

i选择，那么只能dp[i-2]+num[i]
i不选，那么dp[i-1]

所以有：dp[i]=max(dp[i-1],dp[i-2]+num[i])

class Solution:
    # @param num, a list of integer
    # @return an integer
    def rob(self, num):
        if not num: return 0
        n = len(num)
        if n==1: return num[0]
        dp = [0]*n
        dp[0],dp[1] = num[0],max(num[1],num[0])
        for i in xrange(2,n):
            dp[i]=max(dp[i-1],dp[i-2]+num[i])
        return dp[n-1]

213. House Robber II

Note: This is an extension of House Robber.

After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

传送门

题意：和198. House Robber差别在于，这题要求首尾不能同时取到。

思路：和上一题其实一样的，我们只需要考虑[0,n-2]和[1,n-1]两个中最大值即可。。。

class Solution:
    # @param {integer[]} nums
    # @return {integer}
    def rob(self, num):
        if not num: return 0
        n = len(num)
        if n==1: return num[0]
        return max(self.solve(num[1:]),self.solve(num[:-1]))
    
    def solve(self,num):
        if not num: return 0
        n = len(num)
        if n==1: return num[0]
        dp = [0]*n
        dp[0],dp[1] = num[0],max(num[1],num[0])
        for i in xrange(2,n):
            dp[i]=max(dp[i-1],dp[i-2]+num[i])
        return dp[n-1]

221. Maximal Square

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.

For example, given the following matrix:
1
2
3
4
5
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 4.

传送门

题意：给定2D矩阵，求里面1构成的正方形的最大面积。

思路：dp

if matrix[i][j]=='1' dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
else dp[i][j] = 0

Python

class Solution:
    # @param {character[][]} matrix
    # @return {integer}
    def maximalSquare(self, matrix):
        if not matrix: return 0
        m , n = len(matrix),len(matrix[0])
        dp = [[0 if matrix[i][j]=='0' else 1for j in xrange(n)]for i in xrange(m)]
        
        for i in xrange(1,m):
            for j in xrange(1,n):
                if matrix[i][j] =='1': dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
                else: dp[i][j] = 0
        
        ans = max([max(i) for i in dp])
        return ans ** 2

712. Minimum ASCII Delete Sum for Two Strings

Given two strings s1, s2, find the lowest ASCII sum of deleted characters to make two strings equal.

Example 1:

**Input:** s1 = "sea", s2 = "eat"
**Output:** 231
**Explanation:** Deleting "s" from "sea" adds the ASCII value of "s" (115) to the sum.
Deleting "t" from "eat" adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.

Example 2:

**Input:** s1 = "delete", s2 = "leet"
**Output:** 403
**Explanation:** Deleting "dee" from "delete" to turn the string into "let",
adds 100[d]+101[e]+101[e] to the sum.  Deleting "e" from "leet" adds 101[e] to the sum.
At the end, both strings are equal to "let", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee" or "eet", we would get answers of 433 or 417, which are higher.

Note:

0 < s1.length, s2.length <= 1000.
All elements of each string will have an ASCII value in [97, 122].

题目地址：leetcode Minimum ASCII Delete Sum for Two Strings

题目大意：给定两个字符串，要求删掉一些字母，使得它们相等。要求删除字母的ASCII码的和最小。

思路：

显然，删掉的字母越少越好，自然就想到了求最长公共子串。这样，答案就是两个字符串的ASCII码的和 - 公共子串ASCII码的和 * 2

如果有多个子串的话，就取和最大那个即可。

于是，可以类似LCS的解法，设dp[i][j]为s1前i个字符和s2前j个字符的最大公共子串的ASCII码的最大的和

于是有：

s1[i] == s2[j] : dp[i][j] = dp[i-1][j-1] + ascii(s1[i])
s1[i] != s2[j] : dp[i][j] = max(dp[i-1][j], dp[i][j - 1])

C++

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int two_string_sum = 0;
        for (int i = 0; i < s1.length(); i++) two_string_sum += s1[i];
        for (int i = 0; i < s2.length(); i++) two_string_sum += s2[i];

        if (s1.empty()  s2.empty())  return two_string_sum;

        vector<vector<int>> dp(s1.size(),vector<int>(s2.size(),0));
        for (int i = 0; i < s1.size(); i++) {
            dp[i][0] = s1[i] == s2[0] ? s1[i] : 0;
            if (i > 0 && dp[i - 1][0] > dp[i][0]) dp[i][0] = dp[i - 1][0];
        }
        for (int j = 0; j < s2.size(); j++) {
            dp[0][j] = s1[0] == s2[j] ? s2[j] : 0;
            if (j > 0 && dp[0][j - 1] > dp[0][j]) dp[0][j] = dp[0][j - 1];
        }

        for (int i = 1; i < s1.size(); i++) {
            for (int j = 1; j < s2.size(); j++) {
                if (s1[i] == s2[j])
                    dp[i][j] = dp[i - 1][j - 1] + s1[i];
                else
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return two_string_sum - (dp[s1.size() - 1][s2.size() - 1] << 1);
    }
};

Java

class Solution {
    public int minimumDeleteSum(String s1, String s2) {
        int twoStringSum = 0;
        for (int i = 0; i < s1.length(); i++) twoStringSum += s1.charAt(i);
        for (int i = 0; i < s2.length(); i++) twoStringSum += s2.charAt(i);

        if (s1.isEmpty()  s2.isEmpty())
            return twoStringSum;

        int[][] dp = new int[s1.length()][s2.length()];
        for (int i = 0; i < s1.length(); i++) {
            dp[i][0] = s1.charAt(i) == s2.charAt(0) ? s1.charAt(i) : 0;
            if (i > 0 && dp[i - 1][0] > dp[i][0]) dp[i][0] = dp[i - 1][0];
        }
        for (int j = 0; j < s2.length(); j++) {
            dp[0][j] = s1.charAt(0) == s2.charAt(j) ? s2.charAt(j) : 0;
            if (j > 0 && dp[0][j - 1] > dp[0][j]) dp[0][j] = dp[0][j - 1];
        }

        for (int i = 1; i < s1.length(); i++) {
            for (int j = 1; j < s2.length(); j++) {
                if (s1.charAt(i) == s2.charAt(j))
                    dp[i][j] = dp[i - 1][j - 1] + s1.charAt(i);
                else
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return twoStringSum - (dp[s1.length() - 1][s2.length() - 1] << 1);
    }
}

Python

class Solution(object):
    def minimumDeleteSum(self, s1, s2):
        """
        :type s1: str
        :type s2: str
        :rtype: int
        """
        two_sum = sum(ord(c) for c in s1) + sum(ord(c) for c in s2)
        if not s1 or not s2: return two_sum

        dp = [[0] * len(s2) for _ in range(len(s1))]
        dp[0][0] = ord(s1[0]) if s1[0] == s2[0] else 0

        for i in range(1, len(s1)):
            dp[i][0] = max(dp[i - 1][0], ord(s1[i])) if s1[i] == s2[0] else dp[i - 1][0]
        for j in range(1, len(s2)):
            dp[0][j] = max(dp[0][j - 1], ord(s2[j])) if s1[0] == s2[j] else dp[0][j - 1]

        for i in range(1, len(s1)):
            for j in range(1, len(s2)):
                if s1[i] == s2[j]:
                    dp[i][j] = dp[i - 1][j - 1] + ord(s1[i])
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return two_sum - (dp[-1][-1] << 1)

718. Maximum Length of Repeated Subarray

Given two integer arrays A and B, return the maximum length of an subarray that appears in both arrays.

Example 1:
1
2
3
4
5
6
7
**Input:**
A: [1,2,3,2,1]
B: [3,2,1,4,7]
**Output:** 3
**Explanation:** 
The repeated subarray with maximum length is [3, 2, 1].
Note:

1 <= len(A), len(B) <= 1000

0 <= A[i], B[i] < 100

题目地址：leetcode Maximum Length of Repeated Subarray

题目大意: 给定两个数组A和B，求他们最大的公共子数组。

思路：

类似于LCS，这题也是DP

设dp[i][j]为以A[i],B[j]结尾的最大公共子数组的长度。

于是有

if A[i - 1] == B[j - 1] dp[i][j] = dp[i - 1][j - 1] + 1
A[i - 1] != B[j - 1] dp[i][j] = 0

ans则为dp数组的最大值

Java

class Solution {
    public int findLength(int[] A, int[] B) {
        if (A.length == 0  B.length == 0) return 0;
        int[][] dp = new int[A.length + 1][B.length + 1];
        int ans = 0;
        for (int i = 1; i <= A.length; i++) {
            for (int j = 1; j <= B.length; j++) {
                dp[i][j] = A[i - 1] == B[j - 1] ? dp[i - 1][j - 1] + 1 : 0;
                ans = Math.max(ans, dp[i][j]);
            }
        }
        return ans;
    }
}

还可以用滚动数组优化空间复杂度O(n)

Java

class Solution {
    public int findLength(int[] A, int[] B) {
        if (A.length == 0  B.length == 0) return 0;
        int[] dp = new int[B.length + 1];
        int ans = 0;
        for (int i = 1; i <= A.length; i++) {
            for (int j = B.length; j >= 1; j--) {
                dp[j] = A[i - 1] == B[j - 1] ? dp[j - 1] + 1 : 0;
                ans = Math.max(ans, dp[j]);
            }
        }
        return ans;
    }
}

Python

class Solution(object):
    def findLength(self, A, B):
        """
        :type A: List[int]
        :type B: List[int]
        :rtype: int
        """
        dp = [0] * (len(B) + 1)
        ans = 0
        for i in range(1, len(A) + 1):
            for j in range(len(B), 0, -1):
                dp[j] = (dp[j - 1] + 1) if A[i - 1] == B[j - 1] else 0
                ans = max(ans, dp[j])
        return ans

799. Champagne Tower

We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup (250ml) of champagne.

Then, some champagne is poured in the first glass at the top. When the top most glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has it's excess champagne fall on the floor.)

For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.

Now after pouring some non-negative integer cups of champagne, return how full the j-th glass in the i-th row is (both i and j are 0 indexed.)

Example 1: Input: poured = 1, query_glass = 1, query_row = 1 Output: 0.0 Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.

Example 2: Input: poured = 2, query_glass = 1, query_row = 1 Output: 0.5 Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.

Note:

poured will be in the range of [0, 10 ^ 9]. query_glass and query_row will be in the range of [0, 99].

题目地址：leetcode Champagne Tower

题目大意：第0排1个杯子，第1排2个杯子以此类推。当某个杯子装满水，溢出的水均匀的向下一排的两边扩散。给定n杯水，问第i行第j个杯子的满水情况。

思路：直接dp

若dp[i][j] > 1

dp[i + 1][j] += dp[i][j]
dp[i + 1][j + 1] += dp[i][j]

就是说当前的i,j可以流向下一行的第j个和第j+1个

C++

class Solution {
public:
	double champagneTower(int poured, int query_row, int query_glass) {
		vector<vector<double>> dp(query_row + 1, vector<double>(query_row + 1, 0));
		dp[0][0] = poured;
		for (int i = 0; i < query_row; ++i) {
			for (int j = 0; j <= i; ++j) {
				double cur = dp[i][j] > 1 ? (dp[i][j] - 1.0) / 2 : 0;
				dp[i + 1][j] += cur;
				dp[i + 1][j + 1] += cur;
			}
		}
		return min(dp[query_row][query_glass], 1.0);
	}
};

Python

class Solution(object):
    def champagneTower(self, poured, query_row, query_glass):
        """
        :type poured: int
        :type query_row: int
        :type query_glass: int
        :rtype: float
        """
        dp = [[0] * (i + 1) for i in range(query_row + 1)]
        dp[0][0] = poured
        for i in range(query_row):
            for j in range(i + 1):
                cur = (dp[i][j] - 1) / 2.0 if dp[i][j] > 1 else 0
                dp[i + 1][j] += cur
                dp[i + 1][j + 1] += cur
        return min(dp[query_row][query_glass], 1)

另一种写法：

Python

class Solution(object):
    def champagneTower(self, poured, query_row, query_glass):
        """
        :type poured: int
        :type query_row: int
        :type query_glass: int
        :rtype: float
        """
        dp = [[0 for _ in range(query_row + 1)] for i in range(query_row + 1)]
        dp[0][0] = poured
        for i in range(1, query_row + 1):
            for j in range(i + 1):
                dp[i][j] += (max(dp[i - 1][j - 1] - 1, 0) / 2.0) + (max(dp[i - 1][j] - 1, 0) / 2.0)
        return min(dp[query_row][query_glass], 1)

818. Race Car

Your car starts at position 0 and speed +1 on an infinite number line. (Your car can go into negative positions.)

Your car drives automatically according to a sequence of instructions A (accelerate) and R (reverse).

When you get an instruction "A", your car does the following: position += speed, speed *= 2.

When you get an instruction "R", your car does the following: if your speed is positive then speed = -1 , otherwise speed = 1. (Your position stays the same.)

For example, after commands "AAR", your car goes to positions 0->1->3->3, and your speed goes to 1->2->4->-1.

Now for some target position, say the length of the shortest sequence of instructions to get there.

Example 1: Input: target = 3 Output: 2 Explanation: The shortest instruction sequence is "AA". Your position goes from 0->1->3.

Example 2: Input: target = 6 Output: 5 Explanation: The shortest instruction sequence is "AAARA". Your position goes from 0->1->3->7->7->6.

Note:

1 <= target <= 10000.

题目地址：leetcode Race Car

题目大意：你可以做两种操作'A'和‘R', A即position += speed, speed *= 2. R即让你速度反向，并且大小为1. 问你用这两种操作到达target的最小步数。

思路：

DP,设dp[i]为到达i的最小步数。

则对于i = 2^k - 1，走k步即可（没有更优的了）

对于2^(k-1) < i < 2^k

先走到2^(k-1) - 1处(A^(k-1))，然后掉头，然后走A^x, 然后掉头，走dp[i - (2^(k -1) - 1)+ 2^(x) - 1]，所以总共为k-1 + 1 + x + 1 + dp[i - (2^(k -1) - 1)+ 2^(x) - 1]
走到2^k - 1，然后掉头，走dp[2^k -1 - i] 总共 k + 1+ dp[2^k - 1- target]

C++

class Solution {
	int numer_bit(int target) {
		int cnt = 0;
		while (target > 0) {
			++cnt;
			target >>= 1;
		}
		return cnt;
	}

public:
	int racecar(int target) {
		vector<int> dp((target << 1) + 1, INT_MAX >> 1);
		dp[0] = 0;
		for (int i = 1; i <= target; ++i) {
			int k = numer_bit(i);
			if ((i & (i + 1)) == 0)
				dp[i] = k;
			else {
				for (int x = 0; x < k; ++x) {
					int p = i - ((1 << (k - 1)) - 1) + (1 << x) - 1;
					if (p < 0) break;
					dp[i] = min(dp[i], k + x + 1 + dp[p]);
				}
				dp[i] = min(dp[i], k + 1 + dp[(1 << k) - 1 - i]);
			}
		}
		return dp[target];
	}
};

Python

class Solution(object):
    def DP(self, target, dp):
        if dp[target] != -1: return dp[target]
        k = target.bit_length()
        if target == 2 ** k - 1:
            dp[target] = k
        else:
            ans = 0x7fffffff
            for t in range(k - 1):
                remain = target - ((1 << (k - 1)) - 1) + ((1 << t) - 1)
                if remain < 0: break
                ans = min(ans, self.DP(remain, dp) + k + t + 1)
            ans = min(ans, self.DP(((1 << k) - 1) - target, dp) + k + 1)  # A^K R DP[2^k-1 - target]
            dp[target] = ans
        return dp[target]

    def racecar(self, target):
        """
        :type target: int
        :rtype: int
        """
        if target < 1: return 0
        dp = [0] + [-1] * (target << 1)
        return self.DP(target, dp)

更多题解可以查看： https://www.hrwhisper.me/leetcode-algorithm-solution/