『我爱机器学习』深入理解SVM(二) - 核函数和软边距

本文尽可能通俗、详细的介绍支持向量机SVM内容。

包括

• 核函数

• 软边距SVM

• 其它

  • Hinge损失
  • 概率SVM
  • 核化逻辑回归

核函数

若我们将原始数据从\(R^d\)空间通过\(\bf z = \Phi(x)\)映射到高维空间\(R^\tilde d\)以解决线性不可分的问题，则SVM原始问题为：

\[ \begin{align*} \min_{\bf w,b}\hspace{3ex} & \frac{1}{2} {\bf w^Tw}\\ {\rm st.}\hspace{3ex} & y_i({\bf w^T z} + b) \ge 1, \hspace{3ex}i=1,2,\cdots ,n \end{align*} \] SVM的对偶问题为： \[ \begin{align*} \max_{ {\boldsymbol \alpha} }& \hspace{3ex}\sum_{i=1}^n\alpha_i-\frac{1}{2} \sum_{i=1}^n\sum_{j=1}^n \alpha_i\alpha_jy_iy_j{\bf z_i^Tz_j}\\ {\rm s.t.} & \hspace{3ex} \alpha_i \ge 0, i = 1,2,\cdots ,n\\ & \hspace{3ex} \sum_{i=1}^n \alpha_iy_i = 0 \end{align*} \] 上一篇博文最后提到，对偶问题仍然依赖于数据维度\(\tilde d\)，因为有\(\bf z_i^Tz_j\)内积运算。当新空间维度很大，甚至是无穷维的时候，这将成为一个计算的瓶颈。

核技巧和核函数

注意\({\bf z_i^Tz_j = \Phi(x_i)^T \Phi(x_j)}\)的计算顺序如下：

1. 先进行空间变换
2. 进行内积

如果将两步合并，会不会快一点？

林轩田老师举了一个简单的例子（为了简单表示，将\(x_1x_2\)和\(x_2x_1\)都放了进来） \[ \boldsymbol{\Phi}({\bf x}) = (1, x_1, x_2, \ldots, x_d, x_1^2, x_1x_2, \ldots ,x_1x_d, x_2x_1, x_2^2, \ldots ,x_2x_d, \ldots, x_d^2) \] 假设两个数据点\({\bf x, x'}\)进行内积，结果如下（常数项、一次项、二次项） \[ \begin{align*} \boldsymbol{\Phi}({\bf x})^\mathsf{T}\boldsymbol{\Phi}({\bf x}') &= 1 +\sum_{i=1}^dx_ix_i' + \sum_{i=1}^d\sum_{j=1}^dx_ix_jx_i'x_j' \\ &= 1+\sum_{i=1}^dx_ix_i' + \sum_{i=1}^d x_ix_i'\sum_{j=1}^dx_jx_j' \\ &= 1 + {\bf x}^\mathsf{T}{\bf x}' + ({\bf x}^\mathsf{T}{\bf x}')({\bf x}^\mathsf{T}{\bf x}') \end{align*} \] 可以看出，先转换再进行内积的操作和我们直接在原空间进行\(1 + {\bf x}^\mathsf{T}{\bf x}' + ({\bf x}^\mathsf{T}{\bf x}')({\bf x}^\mathsf{T}{\bf x}')\)的内积结果是一样的。

因此，在某些情况下，如果把变换和内积这两个步骤合起来，计算效率可以得到提高。

转换+内积合并为一步称为核技巧，换句话说，核技巧是要找一个核函数K，使得 \[ K_\boldsymbol{\Phi}({\bf x}, {\bf x}') \equiv \boldsymbol{\Phi}({\bf x})^\mathsf{T}\boldsymbol{\Phi}({\bf x}') \] 上面简单的例子中，核函数为 \[ K_{\boldsymbol{\Phi} }({\bf x}, {\bf x}') = 1 + {\bf x}^\mathsf{T}{\bf x}' + ({\bf x}^\mathsf{T}{\bf x}')^2 \] 有了核函数后，可以直接用核函数K在原本的d维空间计算，而不用在高维空间中计算很复杂的内积。

注意到我们的SVM对偶问题中，无论是目标函数还是决策函数，都只有输入实例核实例的内积，因此可以用核函数写为： \[ \begin{align*} \max_{ {\boldsymbol \alpha} }& \hspace{3ex}\sum_{i=1}^n\alpha_i-\frac{1}{2} \sum_{i=1}^n\sum_{j=1}^n \alpha_i\alpha_j y_iy_j K({\bf x_i},{\bf x_j})\\ {\rm s.t.} & \hspace{3ex} \alpha_i \ge 0, i = 1,2,\cdots ,m\\ & \hspace{3ex} \sum_{i=1}^n \alpha_iy_i = 0 \end{align*} \] 而决策函数可以写为： \[ \begin{align}f({\bf {\bf x} }) &= \rm sign \left( {\bf w}^T\Phi({\bf x}) + b \right)\\ &= \rm sign \left( \sum_{i=1}^n \alpha_iy_i\Phi({\bf x}_i)^T \Phi({\bf x}) + b\right)\\ &= \rm sign \left( \sum_{i=1}^n \alpha_iy_iK({\bf x}_i,{\bf x}) + b\right) \\ &= \rm sign \left( \sum_{SV} \alpha_iy_iK({\bf x}_i,{\bf x}) + b\right) \end{align} \]

最后的SV表示支持向量。

于是就得到了核支持向量机。

核函数的选择

SVM引入了核函数之后，摆脱了对映射后高纬度\(\tilde d\)的内积计算。因此在实际问题中，我们通过指定核函数而非映射方式\(\Phi(x)\)。

核函数隐式的定义了一个特征空间，而我们希望在这个特征空间中，我们的样本线性可分。因此核函数的选择是十分重要的，如果核函数选择不合适，意味着将样本映射到了一个不合适的特征空间，很可能性能不佳。

下面介绍常见的多项式核和高斯核。

多项式核

多项式核写作: \[ K({\bf x}, {\bf x}') = (\zeta + \gamma {\bf x^\mathsf{T}x}')^d \tag{1-1} \] 当多项式核中的\(\zeta = 0, \gamma = 1, d = 1\)时，退化为线性核。

下图为林轩田老师给出的多项式核中不同参数的效果，其中带方框的点是支持向量。

Polynomial-kernel

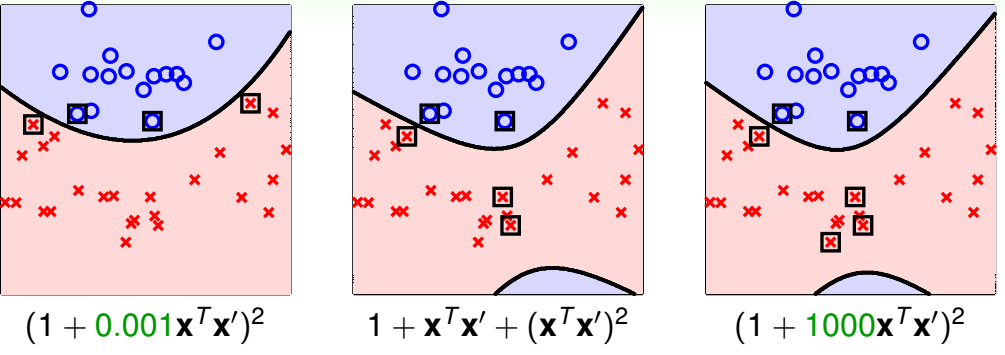
我们很难在训练前说哪一个比较好，往往需要进行交叉验证等来判断。

但是这个例子说明了我们把核函数换掉，SVM的边界也随之改变（说明我们需要进行核函数选择）。在实践中，应记住"linear first"， 从线性核这种简单模型开始尝试。

高斯核

高斯核可以方便的计算无限维度的内积，如下： \[ \begin{align*} K({\bf x}, {\bf x}') &= \exp(-({\bf x}-{\bf x}')^2) \\ &= \exp(-{\bf x}^2)\exp(-{\bf x}'^2)\exp(2{\bf xx'}) \\ &= \exp(-{\bf x}^2)\exp(-{\bf x}'^2)\left(\sum_{i=0}^\infty\frac{(2{\bf xx'})^i}{i!}\right) \hspace{3ex}{\rm Taylor\ 展开} \ \exp(x) = \sum_{n=0}^{\infty} \frac{x^n}{n!}\\ &= \sum_{i=0}^\infty\left(\exp(-{\bf x}^2)\exp(-{\bf x}'^2)\sqrt{\frac{2^i}{i!} }\sqrt{\frac{2^i}{i!} } ({\bf x})^i({\bf x}')^i\right) \\ &= \Phi({\bf x})^\mathsf{T}\Phi({\bf x}') \end{align*} \] 即多项式变换将x映射到一个无限维的空间中： \[ \Phi({\bf x}) = \exp(-{\bf x}^2)\cdot \left(1, \sqrt{\frac{2}{1!} }{\bf x}, \sqrt{\frac{2^2}{2!} }{\bf x}^2,\ldots\right) \] 更一般的，高斯核函数写为： \[ K({\bf x},{\bf x}') = \rm exp \left(- \frac{|\!|{\bf x} - {\bf x}'|\!|^2}{2\sigma^2}\ \right) \tag{1-2} \] 带入核支持向量机得到： \[ \begin{align*} g_{\rm SVM}({\bf x}) &= {\rm sign}\left(\sum_{\rm SV}\alpha_iy_i K({\bf x}_i, {\bf x})+b\right) \\ &= {\rm sign}\left(\sum_{\rm SV}\alpha_iy_i \exp\left(\frac{|\!|{\bf x}-{\bf x}_i|\!|^2}{2\sigma^2}\right)+b\right) \end{align*} \] 上述的式子中，此时SVM实际上是以支持向量为中心的高斯函数的线性组合，因此高斯核函数通常也称为RBF核（Radial Basis Function kernel, Radial 就是长得像高斯函数的(只和\(x_i\)到中心\(x\)的距离有关)，Basis function就是拿来做线性组合的)。

至此，可以小小总结一下我们SVM一路的”进化“：

• 使用\(\bf z = \Phi(x)\) => 高效的核函数K(x, x')

• 保存最优的w， => 保存较少的支持向量和相应的\(\alpha_i\)

而使用高斯核函数可以映射到无限多维空间！而我们的鲁棒性保证则是最大边界的性质。

当然，SVM也是会过拟合的。

林轩田老师又给出了下面的图：

gaussian-kernel-function

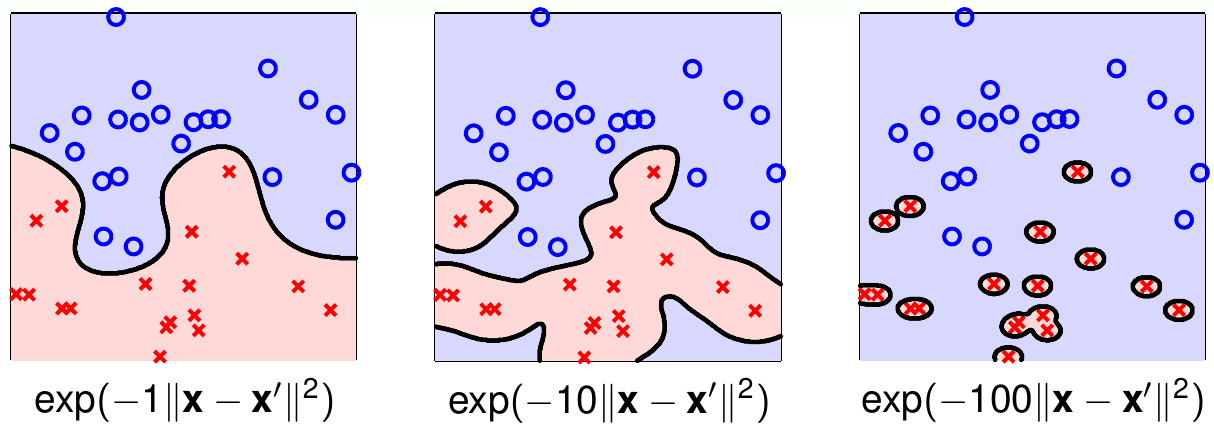
注：林轩田老师的高斯核函数为\(K({\bf x},{\bf x}') = \rm e{\bf x}p \left(- \gamma|\!|{\bf x} - {\bf x}'|\!|^2\ \right)\)，和本文的其实是一样的

可以看出，\(\gamma\)越大，高斯函数越尖锐，模型越容易过拟合。可以想象，当\(\gamma \rightarrow \infty\)时，高斯函数\(K({\bf x}, {\bf x}') = [\![{\bf x} = {\bf x}']\!]\)

核函数比较

• 线性核函数\(K({\bf x, x}') = {\bf x^Tx}'\) 实际上没有进行特征空间变换。最安全也最快。最后得到的模型可解释性强：w会给出每个特征的权重，支持向量会给出每个数据点的重要性。缺点是：数据可能不是线性可分的。对文本数据通常使用线性核函数。
• 多项式核\(K({\bf x}, {\bf x}') = (\zeta + \gamma {\bf x^\mathsf{T}x}')^d\)比线性核更通用，参数d直接描述了被映射空间的复杂度。但它参数较多，调参较难。多项式核可能适用于d比较小的场景，因为当d很大的时候计算不稳定。不稳定表现在：当\(|\zeta + \gamma {\bf x^\mathsf{T}x}' | \lt 1\)时，核函数逼近0，当\(|\zeta + \gamma {\bf x^\mathsf{T}x}' | \gt 1\),核函数值会非常大。
• 高斯核\(K({\bf x},{\bf x}') = \rm e{\bf x}p \left(- \frac{|\!|{\bf x} - {\bf x}'|\!|^2}{2\sigma^2}\ \right)\),可以计算出更复杂的边界，相比多项式核只有一个参数，容易调参。但是由于映射到了无限维空间，没有一个直观的w来解释模型。此外，它的计算也比较复杂，容易过拟合。

核函数的性质

核函数实际上是x和x'映射到新的特征空间的相似度衡量。（向量本身就表示相似性，如正交的时候我们就说一点都不像）。当然不是所有的相似性都能用一个合法的核函数表示。如果一个函数K是合法的核函数，K必须满足下面两个条件（Mercer条件）：

• K是对称的
• K必须是半正定的

此外，核函数还可以通过函数组合得到，

• K1，K2为核函数，对于任意正数\(\gamma_1, \gamma_2\)，其线性组合也是核函数： \(\gamma_1K_1 + \gamma_2K_2\)
• K1，K2为核函数，核函数的直积也是核函数：\(K1\otimes K_2({\bf x,z}) = K_1({\bf x,z})K_2({\bf x,z})\)
• K1为核函数，则对于任意函数g(x)， \(g({\bf x})k_1({\bf x, z})g({\bf z})\)也是核函数

软间隔SVM

前面提到的SVM都是硬间隔的，所谓的硬间隔，就是要求所有的样本都分对，此外还要求每个样本离分离超平面有一定的距离。为了解决线性不可分的情况，使用了核函数进行特征空间的变换，然而，即使我们进行特征空间变换后把样本完全的分开，也有可能这个“线性可分”是因为噪声点而过拟合造成的。（很多情况下，训练数据中有一些噪声点，把这些噪声点去除后，剩下的大部分样本组成的特征空间是线性可分的。）

因此，我们可以对SVM适当的放松条件，不再要求所有的点都分对，而是对不能满足约束的样本进行一些“惩罚”，为此引入惩罚因子\(\xi_i \ge 0\)，并写出软间隔SVM的形式如下： \[ \begin{align*} \min_{ {\bf w}, b,\xi }\hspace{2ex}&\frac{1}{2}{\bf w^Tw} + C\cdot \sum_{i=1}^n \xi_i\\ {\rm s.t.} \hspace{2ex} &y_i({\bf w^\mathsf{T}x}_i + b) \ge 1 -\xi_i \\ \hspace{2ex} &\xi_i \ge0, i=1,2,....,n \end{align*}\tag{2-1} \] C为惩罚参数，C越大说明越不能容忍犯错，尽可能的分对所有的点，C越小说明对错误的容忍程度越大，间隔可以越宽。

下图就直观的描述了软间隔SVM，紫色的violation说明该点在间隔内，而紫色的长度就记录了对间隔的违反程度，即\(\xi_i\)（啰嗦一句，原先我们要求都在间隔外）。

soft-margin-svm

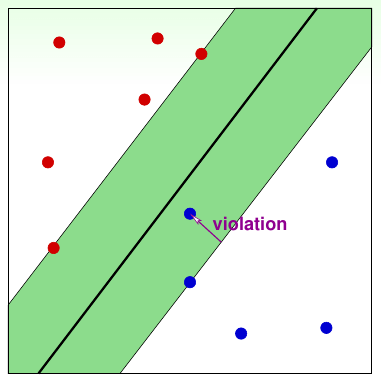
软间隔SVM的对偶问题

和之前硬边界的SVM一样，我们求解对偶问题。

首先同样写出拉格朗日函数： \[ \mathcal{L}({\bf w},b, {\boldsymbol \xi}, {\boldsymbol \alpha}, {\boldsymbol \beta}) = \frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{i=1}^n \xi_i + \sum_{i=1}^n\alpha_i(1 - \xi_i - y_i({\bf w^Tx_i}+b)) -\sum_{i=1}^n\beta_i\xi_i \] \(\mathcal{L}({\bf w},b, {\boldsymbol \xi}, {\boldsymbol \alpha}, {\boldsymbol \beta})\)对\({\bf w}, b, \xi_i\)的极小得 \[ \begin{align*} \frac{\partial \mathcal{L} }{\partial \bf w} &= {\bf w}-\sum_{i=1}^n\alpha_iy_i{\bf x_i} =0\\ \frac{\partial \mathcal{L} }{\partial b } &= -\sum_{i=1}^n\alpha_iy_i =0\\ \frac{\partial \mathcal{L} }{\partial \xi_i} &= C - \alpha_i - \beta_i =0\\ \end{align*} \] 整理得： \[ \begin{align*} {\bf w} =\sum_{i=1}^n\alpha_iy_i{\bf x_i}\\ \sum_{i=1}^n\alpha_iy_i =0\\ C - \alpha_i - \beta_i =0\tag{2-2} \end{align*} \] 带入拉格朗日函数得： \[ \min_{ {\bf w},b, {\boldsymbol \xi} }\mathcal{L}({\bf w},b, {\boldsymbol \xi}, {\boldsymbol \alpha}, {\boldsymbol \beta}) = - \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j{\bf x_i^T x_j} + \sum_{i=1}^n\alpha_i \] 在对\(\min_{ {\bf w},b, {\boldsymbol \xi} }\mathcal{L}({\bf w},b, {\boldsymbol \xi}, {\boldsymbol \alpha}, {\boldsymbol \beta})\)求极大，得到下式： \[ \begin{align*} \max_{ {\boldsymbol \alpha} }\hspace{2ex}& \sum_{i=1}^n\alpha_i - \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j{\bf x_i^T x_j} \\ {\rm s.t.} \hspace{2ex} & \sum_{i=1}^n\alpha_iy_i =0\\ \hspace{2ex} & \alpha_i \ge 0\\ \hspace{2ex} & \beta_i \ge 0\\ \hspace{2ex} & C - \alpha_i -\beta_i = 0\\\tag{2-3} \end{align*} \] 前面提到过，w无关了，所以不写\({\bf w} =\sum_{i=1}^n\alpha_iy_i{\bf x_i}\) 又因为可以利用等式约束去除\(\beta_i\)， \(\beta_i \ge 0 \Rightarrow C - \alpha_i \ge 0\)

于是2-3可以化简为: \[ \begin{align*} \max_{ {\boldsymbol \alpha} }\hspace{2ex}& \sum_{i=1}^n\alpha_i - \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j{\bf x_i^T x_j} \\ {\rm s.t.} \hspace{2ex} & \sum_{i=1}^n\alpha_iy_i =0\\ \hspace{2ex} & 0 \le \alpha_i \le C\tag{2-4} \end{align*} \] 2-4即为我们的软间隔SVM对偶问题。其对应的KKT条件为：

• 主问题可行：\(y_i({\bf w^\mathsf{T}x}_i + b) \ge 1 -\xi_i ; \hspace{2ex} \xi_i \ge 0\)
• 对偶问题可行：\(\alpha_i \ge 0; \hspace{2ex} \beta_i \ge 0\)
• 互补松弛：\(\alpha_i(1 - \xi_i - y_i({\bf w^Tx_i}+b)) = 0; \hspace{2ex} \beta_i\xi_i = 0\)
• 2-2的条件: \({\bf w} = \sum_{i=1}^n\alpha_iy_i{\bf x_i} ; \hspace{2ex} \sum_{i=1}^n\alpha_iy_i =0 ;\hspace{2ex} C - \alpha_i - \beta_i =0\\\)

2-4和硬间隔的对偶SVM对比发现，其实就是多了限制\(\alpha_i \le C\)。

软间隔SVM的支持向量

分析软间隔SVM对偶问题的KKT条件，可以得出结论： - 当\(\alpha_i = 0\) 此时不是支持向量 - 当\(\alpha_i \gt 0 \Rightarrow 1 - \xi_i - y_i({\bf w^Tx_i}+b) = 0\)，此时为支持向量，但可以细分为两种情况 - \(\alpha_i < C \Rightarrow \beta_i\ne0 ; \ \xi_i =0\), 此时样本i正好在间隔上，称为自由的支持向量free support vector。 - \(\alpha_i = C \Rightarrow \beta_i=0 ; \ \xi_i >0\)，此时\({\bf x_i}\)在间隔内，\(\xi_i\)反应了和间隔的距离。称为受限支持向量bounded support vector。此时又分为三种情况： - \(\xi_i \lt 1\) ，分类正确，\({\bf x_i}\)在间隔边界和超平面之间 - \(\xi_i = 1\) ，\({\bf x_i}\)在超平面上 - \(\xi_i \gt 1\) ，分类错误，\({\bf x_i}\)在超平面误分一侧

由此可以看出，软间隔SVM最终模型仅和支持向量有关，引入软间隔后仍保持稀疏性。

下面是林轩田老师给的图，自由支持向量用方框标出，受限支持向量以三角标出。

soft-margin-svm-support-vector

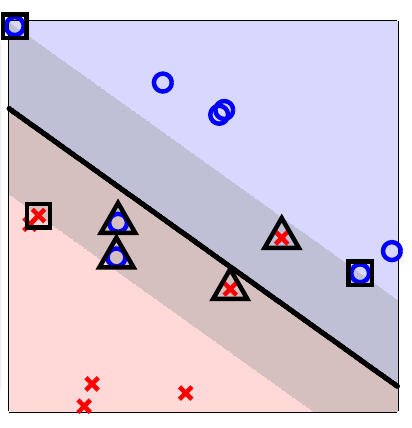
求解对偶问题

假设求解出了\(\alpha\), 那么根据KKT条件, \({\bf w} = \sum_{i=1}^n \alpha_iy_i{\bf x_i}\)

那b呢？模仿之前的硬间隔SVM对偶问题，选取一个\(\alpha_i \gt 0\) 可得\(b = y_i - y_i\xi_i - {\bf w^\mathsf{T}x}_i\)，然而这样需要求解\(\xi_i\),因此可以看看另外一个互补松弛条件。\(\beta_i\xi_i = 0 \Rightarrow (C - \alpha_i)\xi_i = 0\),即当\(\alpha_i \lt C \Rightarrow \xi_i = 0\)，因此选取任意的自由的支持向量即可求解\(b = y_i - {\bf w^\mathsf{T}x}_i\)

当然，极少数的情况下，没有自由的支持向量，那么b就只能通过一系列不等式得出，此时可能有不止一个b存在。

模型选择

值得注意的是，虽然是软间隔，但仍然可能过拟合。

下面是林轩田老师给出的使用高斯核函数的软间隔SVM的不同参数效果图：

soft-margin-svm-gaussian-kernel-parameter

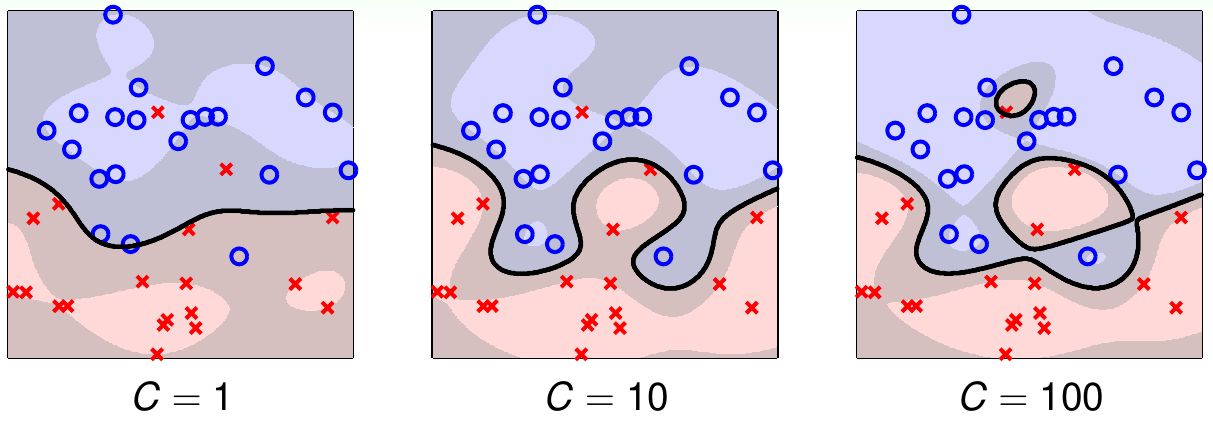
小的C可能会欠拟合，大的C可能会过拟合。因此要小心的选择参数。

如何选择参数呢，常用的就是交叉验证的方法。

这里推导一个有趣的公式---使用留一交叉验证（即样本数m，m折的交叉验证）的留一误差的上界是: \[ \rm E_{LOOCV} =\frac{\text{SV_num}}{m}\tag{2-5} \] 简单证明如下：

• 设总的数据集为\(g\) ，此时验证集为样本点\(({\bf x_n}, y_n)\)
• 若最优的\(\alpha_n = 0\) ,则该点不是支持向量。
  • 若把该点去掉，求解出的\(\{\alpha_1,\alpha_2,\cdots, \alpha_{n-1}\}\)仍然是最优的
  • 也就是去除非支持向量的点求解出的\(g^-\)和不去掉求解出的\(g\)是一样的，又因为非支持向量肯定分类正确，于是有：\(e_{\rm non-SV} = {\rm err}(g^-, {\rm non\text{-}SV}) = {\rm err}(g, {\rm non\text{-}SV}) = 0\)
• 而如果是支持向量有：\(e_{\rm SV} \le 1\)
• 求和取平均得到式2-5

因此，留一交叉验证的error的上界是支持向量个数的比例。如果一个算法的支持向量数比较少，那么它过拟合的风险可能就比较小。因此在调参的时候，可以排除一些支持向量数太多的模型，然后再去验证剩下的模型。

其它

回顾一下软间隔SVM原始问题2-1： \[ \begin{align*} \min_{ {\bf w}, b,\xi}\hspace{2ex}&\frac{1}{2}{\bf w^Tw} + C\cdot \sum_{i=1}^n \xi_i\\ {\rm s.t.} \hspace{2ex} &y_i({\bf w^\mathsf{T}x}_i + b) \ge 1 -\xi_i \\ \hspace{2ex} &\xi_i \ge0, i=1,2,....,n \end{align*} \] \(\xi_i\)描述了对间隔的破坏程度，啰嗦的分析一下有两种情况：

• 该点破坏了间隔边界，\(\xi_i = 1 - y_i({\bf w^T}{\bf x}_i + b) \gt 0\)
• 该点没有破坏边界，\(\xi_i = 0\)

因此，我们可以把软间隔SVM 2-1写为一个没有限制的优化问题： \[ \min_{ {\bf w}, b}\hspace{2ex}\frac{1}{2}{\bf w^\mathsf{T}w} + C\cdot \sum_{i=1}^n \max \left( 1 - y_i({\bf w^T}{\bf x}_i + b) , 0\right)\\ \tag{3-1} \] 如果你学过正则化，会发现上面的式子和正则化是十分相似的，正则化更一般的形式是： \[ \min_f \hspace{2ex} \Omega(f) + C\sum_{i=1}^n l\left( f({\bf x_i}) , y_i\right) \tag{3-2} \] 式3-2中\(\Omega(f)\)称为结构风险，用于描述模型f的某些性质，第二项\(l\left( f({\bf x_i}) , y_i\right)\)则称为经验风险，用于描述模型和训练数据的契合程度。

我们的式3-1的第一项是w的长度，描述了模型本身的复杂度，第二项则是样本中的误差和。换句话说，大间隔其实就是正则化的一种体现，代表选择的超平面要少。而软间隔则是一种特殊的损失函数，称为hinge损失。参数C出现在3-1和3-2中，若C越大，则代表越小的正则化。

将软间隔SVM看作一种正则化，我们可以将其理论延伸到其它模型，与其它模型建立联系。

Hinge损失

上一小节已经剧透过，3-1第二项为hinge损失，其它常见的0-1损失替代函数有：

• hinge损失： \(l_{hinge}(z) = \max \left( 1 - z , 0\right)\)
• 指数损失： \(l_{exp}(z) = \exp(-z)\)
• 对率损失：\(l_{log}(z) = \log(1+\exp(-z))\)

我们什么始化用到这些损失函数呢？ 对率损失其实是逻辑回归采用的，而指数损失将在后面介绍的Adaboost模型中用到。

这里使用了周志华老师的图来作为对比(PS: 该图的log是以2为底的，这样正好为0-1损失的上界):

hinge-exponential-logistic-loss-function

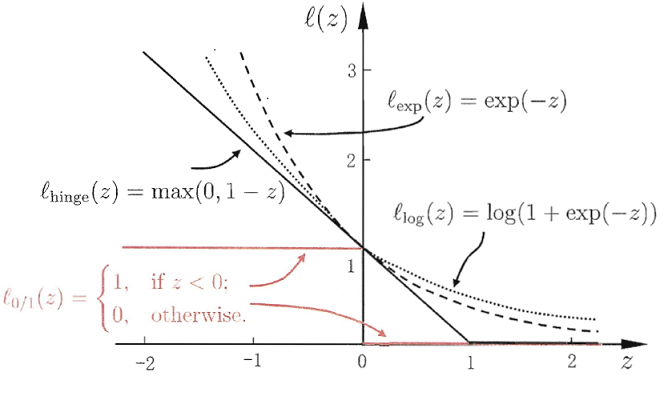
上面提到的hinge、指数、对率损失（以2为底）函数都是0-1损失函数的上界。

hinge和逻辑回归使用的损失函数（对率损失）十分相似：

• 当z趋于正无穷，hinge为0，对率损失约等于0
• 当z趋于负无穷，它们都趋于负无穷。

因此可以把软间隔SVM看作是L2正则化的逻辑回归。而正则化的逻辑回归也像是在做SVM。它们的一些区别和相似周志华老师概况如下：

支持向量机和对率回归的优化目标相近。通常情形下它们的性能也相当。

对率回归的优势主要在于其输出具有自然的的概率意义，即在给出预测标记的同时也给出了概率，而支持向量机的输出不具有概率意义，要得到概率输出需要进行特殊处理。此外对率回归可以直接用于多分类任务，支持向量机为此则需要进行推广[Platt, 2000]。

另一方面，hinge损失有一快“平坦”的区域（就是z >=1），这使得支持向量机的解具有稀疏性。而对率损失函数是光滑的单调递减函数，不能导出类似支持向量的概念，因此，对率回归的解依赖于更多的训练样本，其预测开销更大。

----From《机器学习》 周志华 P132-133

概率SVM--Platt模型

周志华老师上面总结得很好，逻辑回归一个好处就是直接输出概率，现在我们来讨论如何让SVM模型也有概率输出。

有两种naive的想法：

1. 先跑软间隔SVM得到超平面参数w和b，然后将它们直接放在Logistic函数（就是那个s的曲线也叫sigmoid函数）计算。这种做法在实际中效果不错，但是失去了我们推导逻辑回归时采用的最大似然的思想等。
2. 先跑软间隔SVM得到超平面参数w和b，将这个结果作为逻辑回归的初始权重，然后使用逻辑回归算法得到最后的分类函数。但是这种方法和直接使用逻辑回归的方法结果差不多，并且丢失了SVM的核方法等特性。

如果能融合上面两种想法就好了。分析一下：

SVM得到的结果\({\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x})} + b_{\rm SVM}\)本质上是一个分数，把这个分数进行放缩和平移，加大自由度。即\(g({\bf x}) = \theta(A \cdot ({\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x})} + b_{\rm SVM}) + B)\)。然后通过逻辑回归训练A和B两个参数来达到使用MLE的目的和效果。这个算法本质上还是SVM，因此对偶、核技巧都可以使用。从几何上说，SVM找出分割面的法向量，然后用逻辑回归进行平移放缩微调。通常，如果SVM的解比较好，A > 0 而B接近0.

因此，新的问题为： \[ \min_{A,B}\hspace{2ex}\frac{1}{N}\sum_{n=1}^N \log\left(1+\exp\left(-y_n(A\cdot (\underbrace{ {\bf w}_{\rm SVM}^\mathsf{T}{\boldsymbol{\Phi}({\bf x}_n)} + b_{\rm SVM} }_{\boldsymbol{\Phi}_{\rm SVM}({\bf x}_n)}) + B)\right)\right)\tag{3-3} \] 很复杂？其实是两步：

1. 解SVM
2. 解逻辑回归（梯度下降等都行）

这个方法称为Platt模型。

核Logistic回归

上面的问题3-3并没有直接在转换后的空间\(\mathcal{Z}\)求解逻辑回归，而是通过核函数把数据变换到\(\mathcal{Z}\)空间中。由于没有直接在\(\mathcal{Z}\)空间求解逻辑回归，因此可能不是该空间最好的逻辑回归的解。如果要在\(\mathcal{Z}\)空间中找逻辑回归的最优解怎么做？

像SVM一样用核方法？但是逻辑回归不是二次规划问题。

回想之前的SVM，不仅在求解w的时候用到了\(\mathcal{Z}\)空间的内积，更重要的是，在之后预测的时候，将w表示成了一堆已经看过的z的线性组合，即\({\bf w^Tz} + b= \sum_{i=1}^n \alpha_iy_i\Phi({\bf x_i}) \Phi({\bf x}) + b=\sum_{i=1}^n \alpha_iy_iK({\bf x_i,x}) + b\)。换句话说，w表示成了z的线性组合，是能使用核方法的关键。

那么，如果我们的w能被z表示，那不就可以使用核函数了么！

接下来证明如下（这个定理称为表示定理）：

对于任何带有L2正则化的线性模型 \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{n}{\bf w^\mathsf{T}w} + \frac{1}{n}\sum_{i=1}^n {\rm err}(y_i, {\bf w^\mathsf{T}z}_i) \] 其最优的\({\bf w_*}=\sum_{i=1}^n\beta_i{\bf z_i}\)

我们可以将最优的\({\bf w_*}\)分解为两个向量\({\bf w}_{||}\)和\({\bf w}_{\perp}\)，即\({\bf w}_\ast = {\bf w}_{||} + {\bf w}_\perp\)。其中\({\bf w}_{||} \in {\rm span}({\bf z}_i), {\bf w}_{\perp} \perp {\rm span}({\bf z}_i)\)

• 由于正交的内积为0，因此有\({\rm err}(y_n, {\bf w_\ast^\mathsf{T}z}_n) = {\rm err}(y_n, ({\bf w_\|} + {\bf w}_\perp)^\mathsf{T}{\bf z}_n) = {\rm err}(y_n, {\bf w_\|^\mathsf{T}z}_n)\)，即\(\bf w_*\)和\(\bf w_{||}\)有相同的error
• 又因为\({\bf w}_\ast^\mathsf{T}{\bf w}_\ast = {\bf w_\|^\mathsf{T}w_\|} + 2{\bf w_\|^\mathsf{T}w_\perp} + {\bf w_\perp^\mathsf{T}w_\perp} = {\bf w_\|^\mathsf{T}w_\|} + {\bf w_\perp^\mathsf{T}w_\perp} > {\bf w_\|^\mathsf{T}w_\|}\)这意味着\(\bf w_{||}\)比最优的\(\bf w_*\)的目标值更小，是矛盾的，因此\({\bf w}_\perp = {\bf 0}\)
• 所以最优解可以用\(\bf z\)的线性组合表示。由此得证。

接下来定义L2正则项的逻辑回归， \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{n}{\bf w}^\mathsf{T}{\bf w} + \frac{1}{n}\sum_{i=1}^n \log(1+\exp(-y_i{\bf w}^\mathsf{T}{\bf z}_i)) \] 由表示定理，最优的\({\bf w_*}=\sum_{i=1}^n\beta_i{\bf z_i}\)。将该式代入原始问题，可以将原来关于w的问题转化成关于β的问题，即核逻辑回归（Kernel Logistic Regression）： \[ \min_{\boldsymbol{\beta} } \frac{\lambda}{n} \sum_{i=1}^n\sum_{i=1}^n\beta_i\beta_j K({\bf x}_i, {\bf x}_j) + \frac{1}{n}\sum_{i=1}^n\log\left(1+\exp\left(-y_i\sum_{j=1}^n\beta_j K({\bf x}_i, {\bf x}_j)\right)\right)\tag{3-4} \] 这是没有约束的优化问题，可以用梯度下降等方法求解。

林轩田老师讲解了另一个视角来理解核逻辑回归问题：

• 3-4最后一项\(\sum_{j=1}^n\beta_j K({\bf x}_i, {\bf x}_j)\)可以看成是先求\(\bf x_i\)和其它数据点\(\bf x_1,\cdots x_m\)的相似度（前面讲过核函数从某种意义上讲是相似度的一种体现），然后将这个相似度和变量\(\beta\)求内积，其实是一种线性模型。
• 前面的项\(\sum_{i=1}^n\sum_{i=1}^n\beta_i\beta_j K({\bf x}_i, {\bf x}_j)\)写成矩阵的形式是：\(\boldsymbol{\beta}^\mathsf{T}{\rm K}\boldsymbol{\beta}\)，本质上是一个正则化。
• 因此核逻辑回归可以看成是关于\(\beta\)的线性模型，用核函数转换数据，并且用核函数来正则化。(我们原先的理解是将w嵌入到核函数的隐式转换并作L2正则)

核逻辑回归和SVM相比，其系数\(\beta_i\)通常不为0。

参考资料

• 机器学习技法 - 林轩田
• 《统计学习方法》 - 李航
• 《机器学习》 - 周志华
• 《从零构建支持向量机(SVM)》 - 张皓