本文尽可能通俗、详细的介绍支持向量机SVM内容。
包括:
- 核线性回归
- 支持向量机回归SVR
核线性回归
现在我们来讨论回归问题,之前我们讲过带正则项的线性回归(岭回归),现在我们也想要将它核化。能核化的理论依据我们之前已经证明过了,即表示定理:
对于任何带有L2正则化的线性模型 \[ \min_{\bf w}\hspace{2ex}\frac{\lambda}{n}{\bf w^\mathsf{T}w} + \frac{1}{n}\sum_{i=1}^n {\rm err}(y_i, {\bf w^\mathsf{T}z}_i) \] 其最优的\({\bf w_*}=\sum_{i=1}^n\beta_i{\bf z_i}\)
首先写出原始的带正则项的线性回归, 并进行核化,然后写成矩阵的形式: \[ \begin{align*} &\min_{\bf w}\hspace{2ex}\frac{\lambda}{n}{\bf w^\mathsf{T}w} + \frac{1}{n}\sum_{i=1}^n(y_i - {\bf w^\mathsf{T}z}_i)^2 \\ \Rightarrow &\min_{\bf \boldsymbol\beta}\hspace{2ex}\frac{\lambda}{n}\sum_{i=1}^n\sum_{j=1}^n\beta_i\beta_jK({\bf x_i},{\bf x_j}) + \frac{1}{n}\sum_{i=1}^n(y_i - \sum_{j = 1}^n\beta_jK({\bf x_i},{\bf x_j}))^2 \\\Rightarrow &\min_{\bf \boldsymbol\beta}\hspace{2ex}\frac{\lambda}{n} \boldsymbol{\beta}^\mathsf{T}{\rm K}\boldsymbol{\beta} + \frac{1}{n}|\!|{\bf y}- {\bf K}{\boldsymbol \beta} |\!|^2\\ \Rightarrow & \min_\boldsymbol{\beta}\hspace{2ex}\frac{\lambda}{n}\boldsymbol{\beta}^\mathsf{T}{\rm K}\boldsymbol{\beta} + \frac{1}{n}(\boldsymbol{\beta}^\mathsf{T}{\rm K^\mathsf{T}K}\boldsymbol{\beta} - 2\boldsymbol{\beta}^\mathsf{T}{\rm K}^\mathsf{T}{\bf y} + {\bf y^\mathsf{T}y}) \end{align*} \] 对\(\beta\)求偏导,并令偏导为0。注意由Mercer定理知道K为对称的半正定矩阵,得: \[ \begin{align*} \nabla E_{\rm aug}(\boldsymbol{\beta}) &= \frac{2}{n}(\lambda {\rm K^\mathsf{T}I}\boldsymbol{\beta} + {\rm K^\mathsf{T}K}{\boldsymbol{\beta} } - {\rm K^\mathsf{T} }{\bf y}) = \frac{2}{n}{\rm K^\mathsf{T}((\lambda{\rm I+K})\boldsymbol{\beta} - {\bf y})} = 0 \\ &\Rightarrow \boldsymbol{\beta} = (\lambda{\rm I+K})^{-1}{\bf y} \end{align*} \] 因为K为半正定矩阵且\(\lambda \gt 0\),因此\(\lambda{\rm I+K}\)是可逆的。求解该问题复杂度\(O(n^3)\),就是求逆矩阵的复杂度。预测时需要\(O(n)\)的复杂度。
带正则项的线性回归中, \({\bf w} = {\rm (\lambda I + X^\mathsf{T}X)^{-1}X^\mathsf{T} }{\bf y)}\),求解复杂度\(O(d^3 + d^2n)\), 预测时间\(O(d)\)。
核线性回归得到的模型相比带正则项的线性回归来说更灵活,但不适合处理大数据。此外,核线性回归得到的结果时稠密的,因为\(\beta\)和核矩阵K有关,而K中的值基本上不是0(除非两个向量垂直,否则一般不是0)。
支持向量回归SVR
上面提到的核线性回归得到的解不稀疏,计算存储开销大,有没有办法得到稀疏的解呢?
传统的回归模型采用的是模型输出f(x)与真实值y之间的差别计算损失,只有二者完全相同的时候,损失才为0。这样可能太苛刻了,如果适当的放宽条件,假设f(x)和y之间最多有\(\epsilon\)的差距,即当\(|f({\bf x}) - y| > \epsilon\)时才计算损失,即: \[ \rm error(y,f({\bf x})) = \max(0, | f({\bf x}) - y | -\epsilon) \] 这种回归任务称为管道回归(tube regression),对应的损失函数称为 \(\epsilon\)-不敏感损失(\(\epsilon\)-insensitive error)。用大白话说,管道回归希望落在管道内。
周志华老师给出了一个直观的图如下:
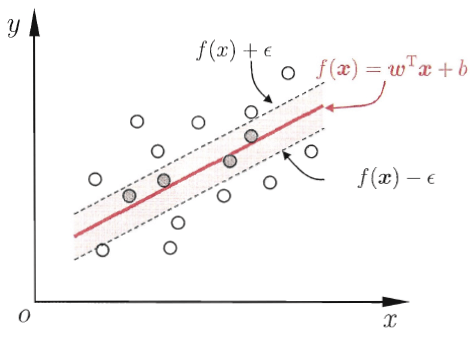
对比均方损失如下图:
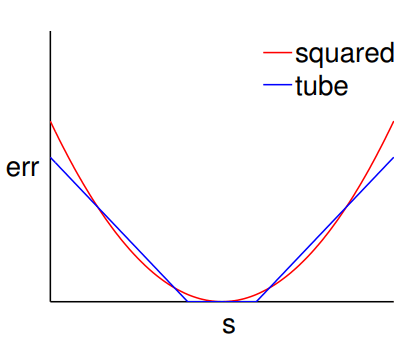
可以看出当\(|f({\bf x}) - y|\)比较小的时候,管道回归的误差与平方误差大致相等。当\(|f({\bf x}) - y|\)比较大时,管道回归的误差又远小于均方误差,说明管道回归的误差受离群点影响更小。
SVR原始问题
管道回归的目标函数可形式化为: \[ \min_{ {\bf w}, b}\hspace{2ex}\frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{i=1}^n\max(0, |{\bf w^\mathsf{T}x}_i+b-y_i|-\epsilon)\tag{2-1} \] 和hinge损失一样,采用了max所以不是处处可微的,因此使用微分的方法会遇到问题。想想软间隔的SVM和采用hinge损失并带正则化的目标函数的转化,是的,引入边界破坏量\(\xi\)我们可以将2-1写成二次规划问题: \[ \begin{align*} \min_{ {\bf w},b, \boldsymbol{\xi} }\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{i=1}^n\xi_i \\ {\rm s.t.}\hspace{2ex}& |y_i -({\bf w^\mathsf{T}x}_i+ b) |\le \epsilon + \xi_i \\ \hspace{2ex}& \xi_i \ge 0, \end{align*} \]
但是这样还不是一个二次规划问题,因为有绝对值,为此需要两个变量: \[ \begin{align*} \min_{ {\bf w},b, \boldsymbol{\xi}^\lor, \boldsymbol{\xi}^\land}\hspace{2ex}&\frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{i=1}^n(\xi_i^\lor + \xi_i^\land) \tag{2-2} \\ {\rm s.t.}\hspace{2ex}& -\epsilon - \xi_i^\lor \le y_i -({\bf w^\mathsf{T}x}_i+ b) \le \epsilon + \xi_i^\land \\ \hspace{2ex}& \xi_i^\lor \ge 0, \\ \hspace{2ex}& \xi_i^\land \ge 0 \end{align*} \] 这里有两个\(\xi\),一个是\(\xi_i^\lor\)一个是\(\xi_i^\land\),分别y在预测值的下方(小于预测值)和在预测值上方(大于预测值f(x))。
SVR对偶问题
到这里应该很熟悉如何推导了吧,毕竟之前已经从硬边距、软边距都推导了一遍。
首先同样写出拉格朗日函数: \[ \begin{align} \mathcal{L}({\bf w},b, {\boldsymbol \xi}^\lor, {\boldsymbol \xi}^\land,{\boldsymbol \alpha}^\lor,{\boldsymbol \alpha}^\land, {\boldsymbol \beta}^\lor,{\boldsymbol \beta}^\land) = \frac{1}{2}{\bf w^\mathsf{T}w} + C\sum_{i=1}^n(\xi_i^\lor + \xi_i^\land) + \sum_{i=1}^n\alpha_i^\land\left(y_i - ({\bf w^T}x_i + b) - \epsilon - \xi_i^\land \right) \\ +\sum_{i=1}^n\alpha_i^\lor\left(-y_i + ({\bf w^T}x_i + b) - \epsilon - \xi_i^\lor \right) - \sum_{i=1}^n\beta_i^\land\xi_i^\land - \sum_{i=1}^n\beta_i^\lor\xi_i^\lor \tag{2-3} \end{align} \]
\(\mathcal{L}({\bf w},b, {\boldsymbol \xi}, {\boldsymbol \alpha}, {\boldsymbol \beta})\)对\({\bf w}, b, \xi_i^\land ,\xi_i^\lor\)求偏导得: \[ \begin{align*} \frac{\partial \mathcal{L} }{\partial \bf w} &= {\bf w}- \sum_{i=1}^n\alpha_i^\land {\bf x_i} +\sum_{i=1}^n\alpha_i^\lor{\bf x_i}=0\\ \frac{\partial \mathcal{L} }{\partial b } &= -\sum_{i=1}^n\alpha_i^\land + \sum_{i=1}^n\alpha_i^\lor =0\\ \frac{\partial \mathcal{L} }{\partial \xi_i^\land} &= C - \alpha_i^\land - \beta_i^\land =0\\ \frac{\partial \mathcal{L} }{\partial \xi_i^\lor} &= C - \alpha_i^\lor - \beta_i^\lor =0\\ \end{align*} \] 整理得: \[ \begin{align*} \tag{2-4} {\bf w} = \sum_{i=1}^n(\alpha_i^\land - \alpha_i^\lor){\bf x_i}\\ \sum_{i=1}^n(\alpha_i^\lor - \alpha_i^\land ) = 0\\ C =\alpha_i^\land + \beta_i^\land \\ C = \alpha_i^\lor + \beta_i^\lor\\ \end{align*} \] 将2-4带入2-3得: \[ \begin{align} \min_{ {\bf w}, b,{\boldsymbol \xi}^\lor, {\boldsymbol \xi}^\land}\mathcal{L}({\bf w},b, {\boldsymbol \xi}^\lor, {\boldsymbol \xi}^\land,{\boldsymbol \alpha}^\lor,{\boldsymbol \alpha}^\land, {\boldsymbol \beta}^\lor,{\boldsymbol \beta}^\land) = \sum_{i=1}^ny_i(\alpha_i^\land - \alpha_i^\lor ) - \epsilon (\alpha_i^\land + \alpha_i^\lor )- \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n(\alpha_i^\land - \alpha_i^\lor )(\alpha_j^\land - \alpha_j^\lor ){\bf x_i^T x_j} \tag{2-5} \end{align} \] 在对2-5求极大得到SVR的对偶问题: \[ \begin{align*} \max_{ {\boldsymbol \alpha^\lor, \alpha^\land} }\hspace{2ex}& \sum_{i=1}^ny_i(\alpha_i^\land - \alpha_i^\lor ) - \epsilon (\alpha_i^\land + \alpha_i^\lor )- \frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n(\alpha_i^\land - \alpha_i^\lor )(\alpha_j^\land - \alpha_j^\lor ){\bf x_i^T x_j} \tag{2-6}\\ {\rm s.t.} \hspace{2ex} & \sum_{i=1}^n(\alpha_i^\lor - \alpha_i^\land ) = 0\\ \hspace{2ex} & 0 \le \alpha_i^\land ,\alpha_i^\lor\le C \end{align*} \] 和以往一样,我们省略2-4中的w,并用等式约束消去了\(\beta_i^\lor, \beta_i^\land\)。
OK,接下来是KKT条件:
- 主问题可行: \(-\epsilon - \xi_i^\lor \le y_i -({\bf w^\mathsf{T}x}_i+ b) \le \epsilon + \xi_i^\land ;\hspace{2ex} \xi_i^\lor \ge 0; \hspace{2ex} \xi_i^\land \ge 0\)
- 对偶问题可行: \(\alpha_i^\land ,\alpha_i^\lor \ge 0; \hspace{2ex} \beta_i^\lor, \beta_i^\land \ge0\)
- 互补松弛:\(\alpha_i^\land\left(y_i - ({\bf w^T}x_i + b) - \epsilon - \xi_i^\land \right) =0; \hspace{2ex} \alpha_i^\lor\left(-y_i + ({\bf w^T}x_i + b) - \epsilon - \xi_i^\lor \right)=0; \hspace{2ex} \beta_i^\land\xi_i^\land = 0 \hspace{2ex} \beta_i^\lor\xi_i^\lor = 0\)
- 2-4的条件\({\bf w} = \sum_{i=1}^n(\alpha_i^\land - \alpha_i^\lor){\bf x_i}; \hspace{2ex} \sum_{i=1}^n(\alpha_i^\lor - \alpha_i^\land ) = 0 ; \hspace{2ex} C =\alpha_i^\land + \beta_i^\land; \hspace{2ex} C = \alpha_i^\lor + \beta_i^\lor\)
此外,还加上两条:\(\alpha_i^\land \alpha_i^\lor = 0; \hspace{2ex}\xi_i^\land \xi_i^\lor = 0;\)这是因为y不可能同时出现在预测值f(x)的上方和下方,因此它们至少一个为0。
稀疏性讨论
SVR的目的是想要一个稀疏的解。那么我们根据对偶问题求解出的是稀疏的么?
前面的KKT可知 \({\bf w} = \sum_{i=1}^n(\alpha_i^\land - \alpha_i^\lor){\bf x_i}\),记\(\beta_i = \alpha_i^\land - \alpha_i^\lor\) 要证明的就是\(\beta_i\)组成的向量\(\boldsymbol \beta\)是稀疏的。
对于在管道中的可以利用互补松弛性可以做如下推导: \[ \begin{align*} & |{\bf w^Tx_i } +b - y_i | \lt \epsilon \\ \Rightarrow \hspace{1ex}& \xi_i^\lor = \xi_i^\land = 0\\ \Rightarrow \hspace{1ex}& y_i - ({\bf w^T}x_i + b) - \epsilon - \xi_i^\land \ne0; \hspace{2ex} -y_i + ({\bf w^T}x_i + b) - \epsilon - \xi_i^\lor \ne0;\\ \Rightarrow \hspace{1ex} &\alpha_i^\land =0 ; \hspace{2ex}\alpha_i^\lor=0\\ \Rightarrow \hspace{1ex} &\beta_i = \alpha_i^\land - \alpha_i^\lor = 0\\ \end{align*} \] 只有不在管道中\(\beta_i \ne 0\),此时为支持向量。显然SVR的支持向量仅为训练样本的一部分,即其解具有稀疏性。
核函数
SVR仍可以核函数: \[ \begin{align*} f({\bf x}) &= {\bf w^Tx} + b \\&= \sum_{i=1}^n(\alpha_i^\land - \alpha_i^\lor){\bf x_i^Tx} + b \\&= \sum_{i=1}^n(\alpha_i^\land - \alpha_i^\lor){\bf K}({\bf x_i},{\bf x}) + b \end{align*} \]
常见分类、回归性能比较
图来自林轩田老师:
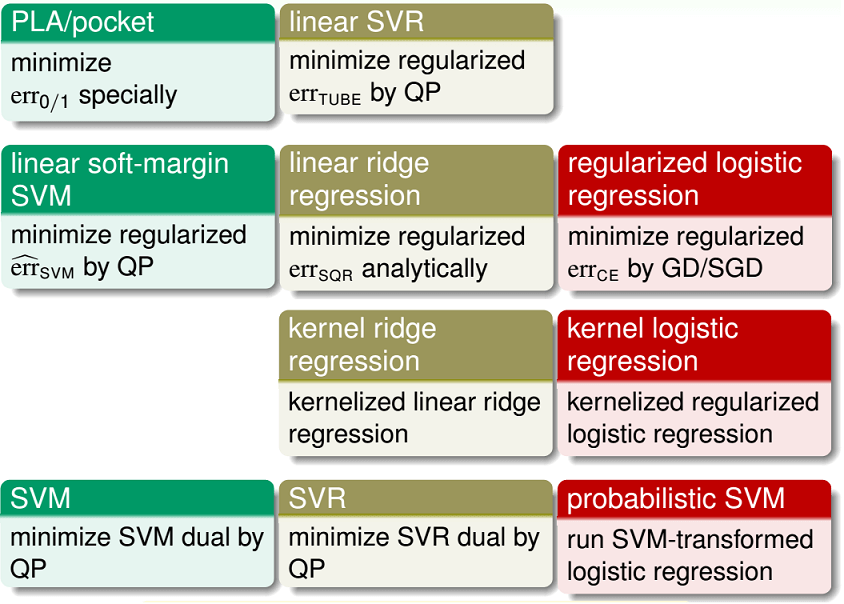
前两行均为线性模型,其中 - 第一行较少使用,因为性能/效果比较差 - 第二行是经典机器学习包liblinear的主力
后两行均为核模型,其中 - 第三行较少使用,因为支持向量是稠密的 - 第四行是经典机器学习包libsvm的主力
参考资料
- 机器学习技法 - 林轩田
- 《机器学习》 - 周志华

